1 模型介绍
模型参考这里。
2 部分代码
clear;
clc;
%jsp_pso
PAR_NUM=50;
GEN_NUM=1000;
JOB_NUM=6;
MAC_NUM=6;
%初始化
n=JOB_NUM*MAC_NUM;
particle=rand(PAR_NUM,n+1);
vel=rand(PAR_NUM,n);
%evaluate
for i=1:PAR_NUM
[A B]=sort(particle(i,1:n));
array=ceil(B/MAC_NUM);
makespan=jp_makespan(array);
particle(i,n+1)=makespan;
end
pbest_p=zeros(PAR_NUM,n);
gbest_p=zeros(1,n); %pbest_p和gbest_p分别代表单个粒子最优序列和种群最优序列;
pbest_v=zeros(PAR_NUM,1);
gbest_v=zeros(1,1); %pbest_v和gbest_v分别代表单个粒子和种群的最小makespan;
for i=1:PAR_NUM
pbest_p(i,1:n)=particle(i,1:n);
pbest_v(i)=particle(i,n+1);
end
[I J]=sort(particle(:,n+1));
gbest_p=particle(J(1),1:n);
gbest_v=particle(J(1),n+1);
e=0.729;
k1=2;
k2=2.1;
iter=0;
while iter<GEN_NUM
for i=1:PAR_NUM
%update
A=rand(1);
B=rand(1);
vel(i,:)=e*vel(i,:)+k1*A*(pbest_p(i,:)-particle(i,1:n))+k2*B*(gbest_p-particle(i,1:n));
particle(i,1:n)=particle(i,1:n)+vel(i,:);
%evaluate
[G H]=sort(particle(i,1:n));
array=ceil(H/MAC_NUM);
makespan=jp_makespan(array);
particle(i,n+1)=makespan;
if particle(i,n+1)<pbest_v(i)
pbest_p(i,:)=particle(i,1:n);
pbest_v(i)=particle(i,1+n);
end
function makespan=jp_makespan(array) % 计算每个粒子的makespan;
%array 表示编码序列;
T=[1 3 6 7 3 6
8 5 10 10 10 4
5 4 8 9 1 7
5 5 5 3 8 9
9 3 5 4 3 1
3 3 9 10 4 1];
js=[3 1 2 4 6 5
2 3 5 6 1 4
3 4 6 1 2 5
2 1 3 4 5 6
3 2 5 6 1 4
2 4 6 1 5 3]; %js矩阵记录每个工件不同工序的加工机床;
wpn=length(array);
[m n]=size(T);
jp=zeros(1,n); %jp记录工件的工序
mp=zeros(1,m); %mp记录机床上的工序
t1_start=zeros(m,n);
t1_end=zeros(m,n); %记录机器每个工序的开始和结束的时间;
t2_start=zeros(m,n);
t2_end=zeros(m,n); %记录工件每个工序的开始时间和结束时间;
for i=1:wpn
k=array(i); %k=1,2,3,4,5,6; 代表工件号;
jp(k)=jp(k)+1; %jp记录工件的工序;
mp(js(k,jp(k)))=mp(js(k,jp(k)))+1; %mp记录机床的工序;
q=mp(js(k,jp(k)));
if jp(k)==1
if mp(js(k,1))==1
t1_start(js(k,1),1)=0;
t1_end(js(k,1),1)=T(k,1);
t2_end(k,1)=t1_end(js(k,1),1);
else
t1_start(js(k,1),mp(js(k,1)))=t1_end(js(k,1),mp(js(k,1))-1);
t1_end(js(k,1),mp(js(k,1)))= t1_start(js(k,1),mp(js(k,1)))+T(k,1);
t2_end(k,1)=t1_end(js(k,1),mp(js(k,1)));
end
unction gant6c6(jobname,t_start,t_end,gbest_v)
[m n]=size(t_start);
axis_size=[0 gbest_v+2 0 m+0.5];
axis(axis_size);
yla=[1:m];
set(gca,'ytick',yla);
ylabel('Processing Machine','FontSize',12,'color','b');
xlabel('Processing Time','FontSize',12,'color','b');
title('the scheduling result','FontSize',16,'color','r');
set(gcf,'Color','g')
hold on
ZO=m+1;
for i=1:m
for j=1:n
x=[t_start(i,j) t_start(i,j) t_end(i,j) t_end(i,j)];
y=[ZO-i-0.3 ZO-i+0.3 ZO-i+0.3 ZO-i-0.3];
% [1 1 0 ] y yellow
% [1 0 1] m magenta
% [0 1 1] c cyan
% [1 0 0] r red
%[0 1 0] g green
%[0 0 1] b blue
switch(jobname(i,j))
case 1
fill(x,y,'y');
case 2
fill(x,y,'m');
case 3
fill(x,y,'c');
case 4
fill(x,y,'r');
case 5
fill(x,y,'g');
case 6
fill(x,y,'b');
end
![]()
3 运行结果
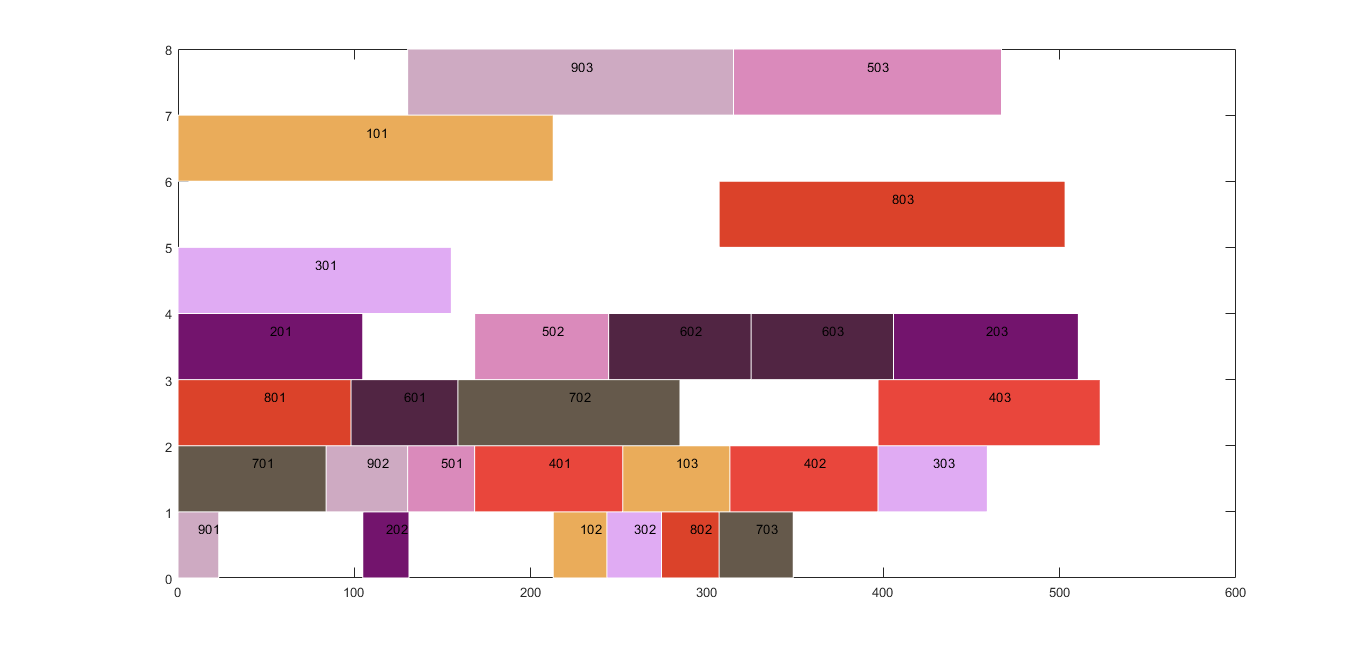
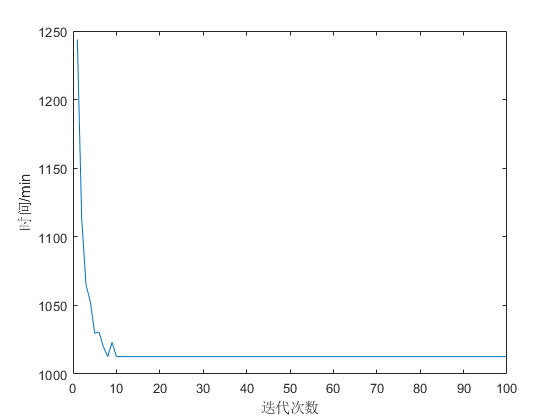
参靠文献
[1]谷峰, 陈华平, 卢冰原,等. 粒子群算法在柔性工作车间调度中的应用[J]. 系统工程, 2005(09):24-27
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。











