下降路径最小和

• 1. 题目解析
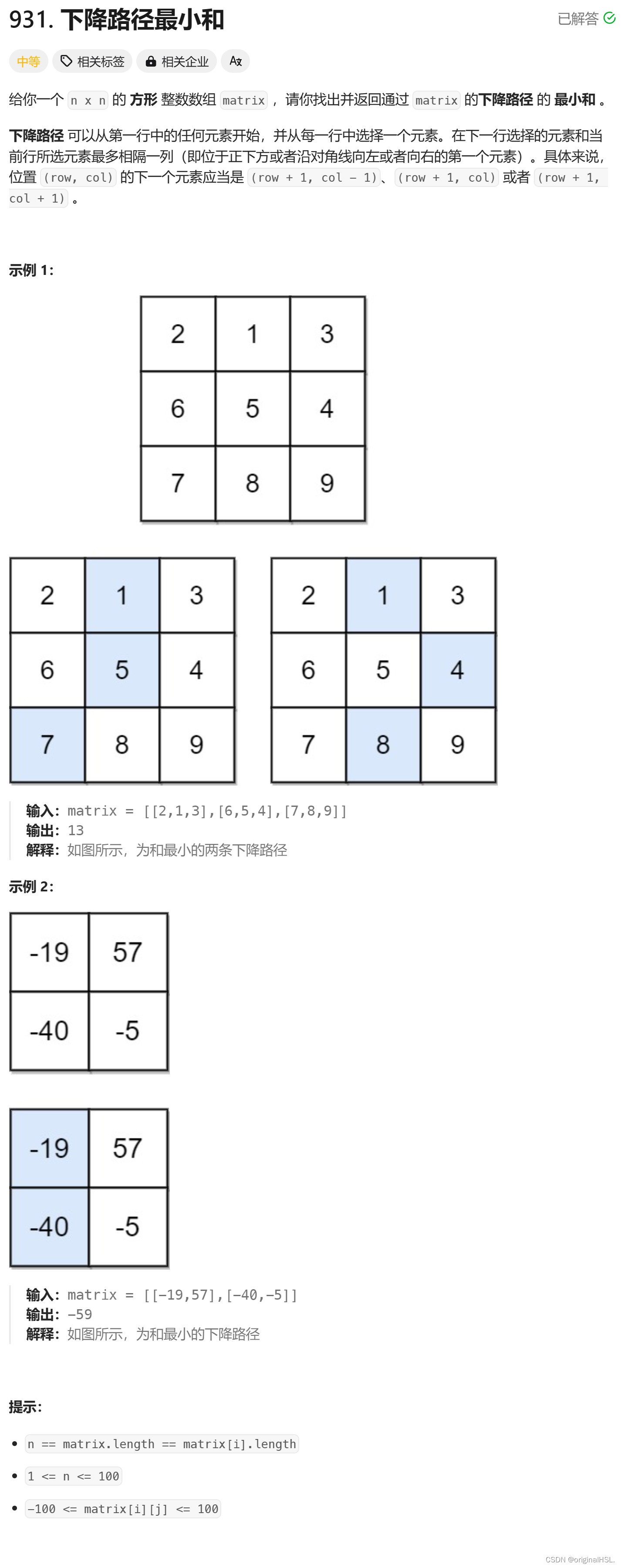
• 2. 讲解算法原理
• • 方法一
  • 方法二
• 3. 编写代码
• • 法一
  • 法二

1. 题目解析

2. 讲解算法原理

方法一

1. 首先，通过matrix的大小确定矩阵的行数m和列数n。

2. 创建一个大小为(m+1) × (n+2)的二维动态规划数组dp，其中dp[i][j]表示从顶部到达矩阵位置(i-1, j-1)的最小下降路径和。

3. 初始化动态规划数组的第一行为0，表示从顶部开始的路径和为0。

4. 从矩阵的第二行开始，依次填表。对于每个位置(i, j)，计算dp[i][j]的值：

• 选择上一行相邻的三个位置(i-1, j-1)、(i-1, j)、(i-1, j+1)中的最小值，记为t。
• 如果t等于0，表示上一行的三个相邻位置都为0，说明当前位置(i, j)无法从上一行的相邻位置下降到达，需要选择其他路径。
  • 如果(i-1, j-1)为0，说明只能选择(i-1, j)和(i-1, j+1)中的较小值作为t。
  • 否则，选择(i-1, j-1)和(i-1, j)的较小值作为t。
• 将当前位置的值matrix[i-1][j-1]与t相加，得到从顶部到达当前位置的最小路径和，并将其赋给dp[i][j]。

5. 在最后一行，遍历所有位置(m, i)，找到最小的路径和，并将其存储在变量min中。

6. 返回变量min，即从顶部到底部的最小下降路径和。

方法二

1. 首先，通过matrix的大小确定矩阵的行数n。

2. 创建一个大小为(n+1) × (n+2)的二维动态规划数组dp，其中dp[i][j]表示从顶部到达矩阵位置(i-1, j-1)的最小下降路径和。

3. 初始化动态规划数组的第一行为0，表示从顶部开始的路径和为0。

4. 从矩阵的第二行开始，依次填表。对于每个位置(i, j)，计算dp[i][j]的值：

• 选择上一行相邻的三个位置(i-1, j-1)、(i-1, j)、(i-1, j+1)中的最小值，记为t。
• 将当前位置的值matrix[i-1][j-1]与t相加，得到从顶部到达当前位置的最小路径和，并将其赋给dp[i][j]。

5. 在最后一行，遍历所有位置(n, j)，找到最小的路径和，并将其存储在变量ret中。

6. 返回变量ret，即从顶部到底部的最小下降路径和。

3. 编写代码

法一

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+2));
        
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                int t=min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]));
                if(t==0) 
                {
                    if(dp[i-1][j-1==0])t=min(dp[i-1][j],dp[i-1][j+1]);
                    else t=min(dp[i-1][j-1],dp[i-1][j]);
                }
                dp[i][j]=matrix[i-1][j-1]+t;
            }
        }
        int min=INT_MAX;
        for(int i=1;i<=n;i++)
        {
            if(dp[m][i]<min)
            min=dp[m][i];
        }
        return min;
    }
};

法二

class Solution
{
public:
    int minFallingPathSum(vector<vector<int>>& matrix) 
    {
        // 1. 创建 dp 表
        // 2. 初始化
        // 3. 填表
        // 4. 返回结果
        int n = matrix.size();
        vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));
        // 初始化第⼀⾏
        for(int j = 0; j < n + 2; j++) dp[0][j] = 0;
        for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
        dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i - 1][j - 1];

        int ret = INT_MAX;
        for(int j = 1; j <= n; j++)
        ret = min(ret, dp[n][j]);
        
        return ret;
    }
};