目录

• 1.介绍
• 2.可以做的题型
• 3.实战
• • 3.1求pi的值
  • 3.2求定积分x^2 的值

1.介绍

2.可以做的题型

3.实战

3.1求pi的值

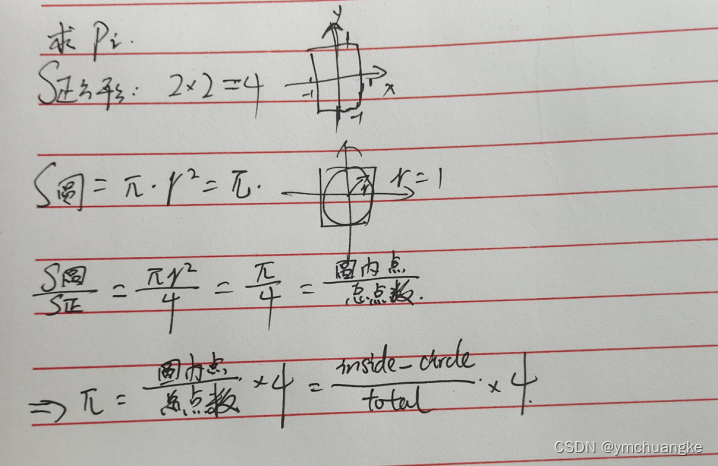
import random #导入random生成随机数

#d定义一个估计pi的函数，传入形参num_saamples
def estimate_pi(num_samples):
    # 定义变量
    inside_circle = 0  #园内点数
    total = 0  #总点数


    #定义for循环，下划线表示在循环中未使用这个变量的值
    #正常for应该是for 变量 in xxx（范围）：
    for _ in range(num_samples):
        #定义xy坐标，正方形面积为2*2=4
        x = random.uniform(-1, 1) #random随机函数
        y = random.uniform(-1, 1)

        #求距离
        distance = x ** 2 + y ** 2

        #判断
        if distance <= 1: #园内点
            inside_circle += 1 #园内加一
        total += 1 #循环一次，总点数加一

    pi_estimate = 4 * inside_circle / total #pi的估计值
    return pi_estimate  #这个函数返回的是pi的估计值

num_samples = 100000 #定义循环次数
pi = estimate_pi(num_samples) #求pi的估计值
print("Estimated value of pi:", pi) #打印pi的估计值

3.2求定积分x^2 的值

import random #导入random

def monte_carlo_integration(func, a, b, num_samples): #定义求取定积分的函数，传入形参func，a，b，numsamples
    total = 0.0 #定义浮点型变量
    for _ in range(num_samples):
        # 定义一个循环，只需要循环，不需要值，用c的话相当于
        #for(int i=0;i<=inum_samples;i++;)

        x = random.uniform(a, b) #产生一个【0，1】的数
        total += func(x)  #算函数值累计求和
    average = total / num_samples #求平均
    integral = average * (b - a) #算面积（积分值）
    return integral #返回积分值

def f(x): #定义一个函数，返回x^2的值
    return x**2

a = 0
b = 1
num_samples = 100000

integral = monte_carlo_integration(f, a, b, num_samples) #形参传入函数的名字，a,b，num_samples
print("The integral of f(x) = x^2 from", a, "to", b, "is approximately:", integral)