目录

• • 1.背景
  • 2.算法原理
  • • 2.1算法思想
    • 2.2算法过程
  • 3.结果展示
  • 4.参考文献

1.背景

2017年，AAA Mohamed等人受到飞蛾趋光行为启发，提出了蛾群算法（Moth Swarm Algorithm, MSA）。

2.算法原理

2.1算法思想

MSA设待优化问题的可行解和适应度函数值分别由光源位置和光源发光强度表示，主要分为：勘探蛾、探测蛾和观察蛾。

• 勘探蛾：能够在优化空间上发现新的区域，引导作用
• 探测蛾：在光源附近区域内漫游到随机螺旋路径中一组已被勘探蛾标识的蛾群
• 观察蛾：一组由探测蛾获得并直接向最佳全局解漂游的蛾群

在每次迭代中，粒子群算法中，蛾群中最佳适应度值被视为勘探蛾空间位置的发光强度，领导下一次更新迭代；而次优的适应度值分别定义为探测蛾和观察蛾。（有点像灰狼算法GWO机制）

2.2算法过程

MSA提出交叉点多样性指数，对于第t次迭代j维蛾群个体归一化分散度：
$${\sigma }_j^t=\frac{\sqrt{\frac{1}{n_p}{\sum }_{i=1}^{n_p}(x_{ij}^t-\overline{x_j^t}{)}^2}}{\overline{x_j^t}}\text{\hspace{1em}(1)}$$
$$\overline{x_j^t}=\sum _{i=1}^{n_p}{x}_{ij}^t\text{\hspace{1em}(2)}$$
其中，np表示勘探蛾数量。
相对分散度表述为：
$${\mu }^t=\frac{1}{d}\sum _{j=1}^d{\sigma }_j^t\text{\hspace{1em}(3)}$$
任何勘探蛾的组成都会受到低分散度的影响，即勘探蛾数量在交叉点cp中被确认：
$$i\in c_{p}if{\sigma }_j^t⩽{\mu }^t\text{\hspace{1em}(4)}$$
差异向量莱维突变：
v p t → = L p 1 t ∙ ( x r t 2 → , x r t 3 → ) + L p 2 t ∙ ( x r t 4 → , − , x r t 5 → ) ∀ r 1 ≠ r 2 ≠ r 3 ≠ r 4 ≠ r 5 ≠ p ≠ ∈ { 1 , 2 , … , n p } x r 1 t → (5) \begin{gathered} \\ \overrightarrow{v_{p}^{t}}=L_{p1}^{t}\bullet(\overrightarrow{x_{r}^{t_{2}}},\overrightarrow{x_{r}^{t_{3}}})+L_{p2}^{t}\bullet(\overrightarrow{x_{r}^{t_{4}}},-,\overrightarrow{x_{r}^{t_{5}}}) \\ \forall r^1\neq r^2\neq r^3\neq r^4\neq r^5\neq p\neq\in \{1,2,\ldots,n_p\} \overrightarrow{x_{r^1}^t} \end{gathered}\tag{5} vpt​ ​=Lp1t​∙(xrt2​​ ​,xrt3​​ ​)+Lp2t​∙(xrt4​​ ​,−,xrt5​​ ​)∀r1=r2=r3=r4=r5=p=∈{1,2,…,np​}xr1t​ ​​(5)
自适应交叉操作,为了获得全局最优解，勘探蛾个体通过子跟踪向量交叉操作更新其位置:
$$V_{pj}^t=\{\begin{array}{l}{v}_{pj}^t\text{if}j\in c_p\\ x_{pj}^t\text{if}j\notin c_p\end{array}\text{\hspace{1em}(6)}$$
选择策略,利用适应度函数值选择下一次迭代操作:
$$x_p^{t+1}=\{\begin{array}{l}{x}_p^t\text{if}f(V_p^t)⩾f(x_p^t)\\ v_p^t\text{if}f(V_p^t)<f(x_p^t)\end{array}\text{\hspace{1em}(7)}$$
概率值Pp与发光强度fitp成比例：
$$P_p=\frac{fi{t}_p}{{\sum }_{p=1}^{n_p}fi{t}_p}\text{\hspace{1em}(8)}$$
MSA通过将锥形顶点保持在固定角度，将蛾群朝向光源的飞行路径描述为围绕锥体表面的一组轨迹，将具有次发光强度的蛾群定义为探测蛾:
$$n_f=\mathrm{round}((n-n_p)\times (1-\frac{t}{T}))\text{\hspace{1em}(9)}$$
探测蛾个体xi根据下式螺旋飞行路径更新其位置:
x i t + 1 = ∣ x i t − x p t ∣ ∙ e θ ∙ c o s 2 π θ + x p t ∀ p ∈ { 1 , 2 , ⋅ ⋅ ⋅ , n p } ; i ∈ { n p + 1 , n p + 2 , ⋅ ⋅ ⋅ , n f } (10) x_{i}^{t+1} = | x_{i}^{t}-x_{p}^{t} | \bullet e^{\theta} \bullet \mathrm{cos}2\pi\theta+x_{p}^{t}\\\forall p\in\{1,2,\cdotp\cdotp\cdotp,n_p\};i\in\{n_p+1,n_p+2,\cdotp\cdotp\cdotp,n_f\}\tag{10} xit+1​=∣xit​−xpt​∣∙eθ∙cos2πθ+xpt​∀p∈{1,2,⋅⋅⋅,np​};i∈{np​+1,np​+2,⋅⋅⋅,nf​}(10)
每种飞蛾类型是动态变化的，任何探测蛾发现比当前位置更佳的光源位置，探测蛾将被替换为勘探蛾。

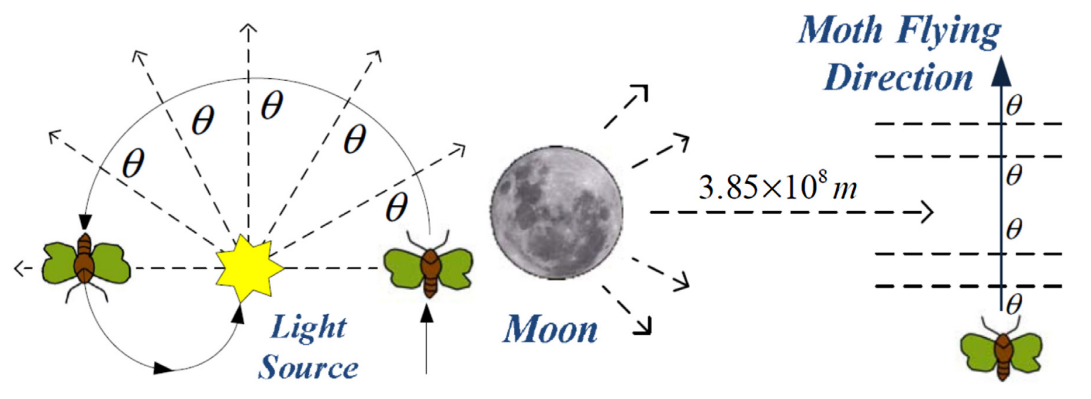
蛾群中具有最低发光强度的蛾被认为是 观察蛾，这些蛾群旨在直接向最佳全局解漂游，新观察蛾进行高斯游走：
x i t + 1 = x i t + ε 1 + [ ε 2 × b e s t g t − ε 3 × x i t ] ∀ i ∈ { 1 , 2 , ⋯   , n G } ε 1 ∼ r a n d o m ( s i z e ( d ) ) ⊕ N ( b e s t g t , log ⁡ t t × ( x i t − b e s t g t ) ) (11) \begin{gathered} x_{i}^{t+1} = x_{i}^{t}+\varepsilon_{1}+\left[\varepsilon_{2}\times best_{g}^{t}-\varepsilon_{3}\times x_{i}^{t}\right] \\ \forall i\in\{1,2,\cdots,n_{G}\} \\ \varepsilon_{1}\sim\mathrm{random}(\mathrm{size}(d))\oplus \\ N\left(best_g^t,\frac{\log t}{t}\times(x_i^t-best_g^t) \right) \end{gathered}\tag{11} xit+1​=xit​+ε1​+[ε2​×bestgt​−ε3​×xit​]∀i∈{1,2,⋯,nG​}ε1​∼random(size(d))⊕N(bestgt​,tlogt​×(xit​−bestgt​))​(11)
观察蛾位置更新：
$$\begin{gathered} x_i^{t+1}=x_i^t+0.001\bullet T[x_i^t-x_i^{\min },x_i^{\max }-x_i^t]+ \\ (1-t/T)\bullet r_1\bullet (bes{t}_p^t-x_i^t)+2t/T\bullet r_2\bullet (bes{t}_p^t-x_i^t)\text{\hspace{1em}(12)} \end{gathered}$$

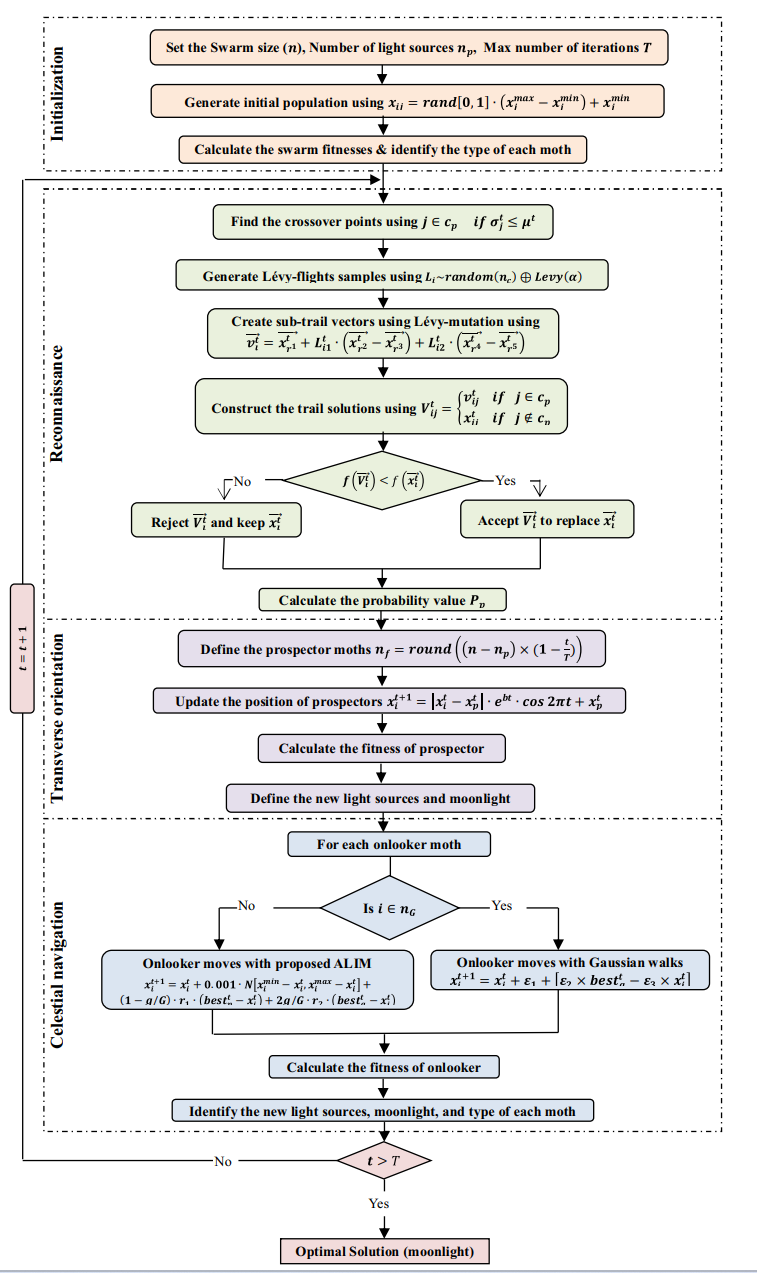
流程图：

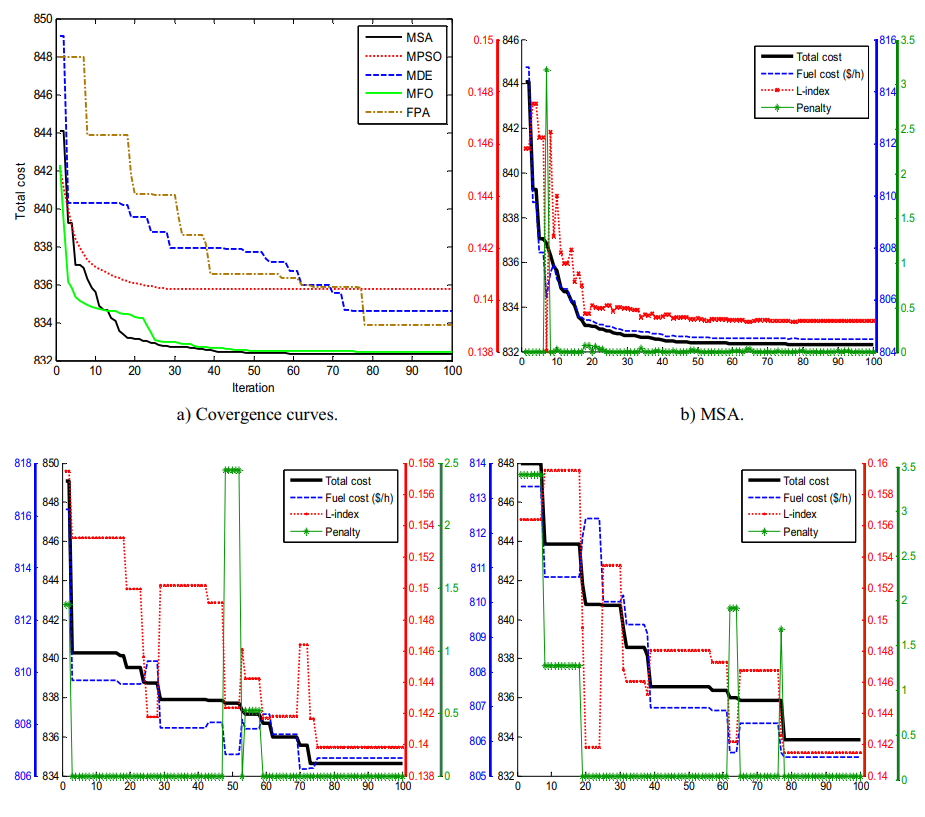
3.结果展示

4.参考文献

[1] Mohamed A A A, Mohamed Y S, El-Gaafary A A M, et al. Optimal power flow using moth swarm algorithm[J]. Electric Power Systems Research, 2017, 142: 190-206.