课件链接(提取码:I786)
1、时间复杂度、空间复杂度
时间复杂度

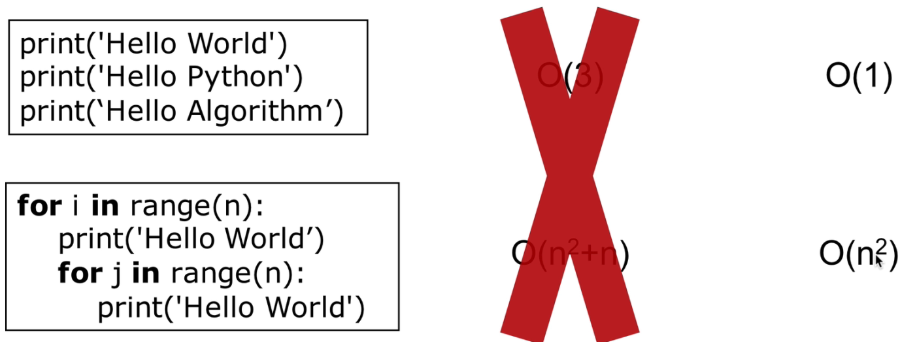




2、递归
斐波拉契数列
汉诺塔
3、查找
3.1 什么是查找

3.2 顺序查找

3.3 二分查找

二分查找要求列表是有序列表,所以受到限制,二分查找的实际复杂度应该是排序的复杂度+查找的复杂度
python内置的查找位置的函数index()使用的是线性查找
4、排序


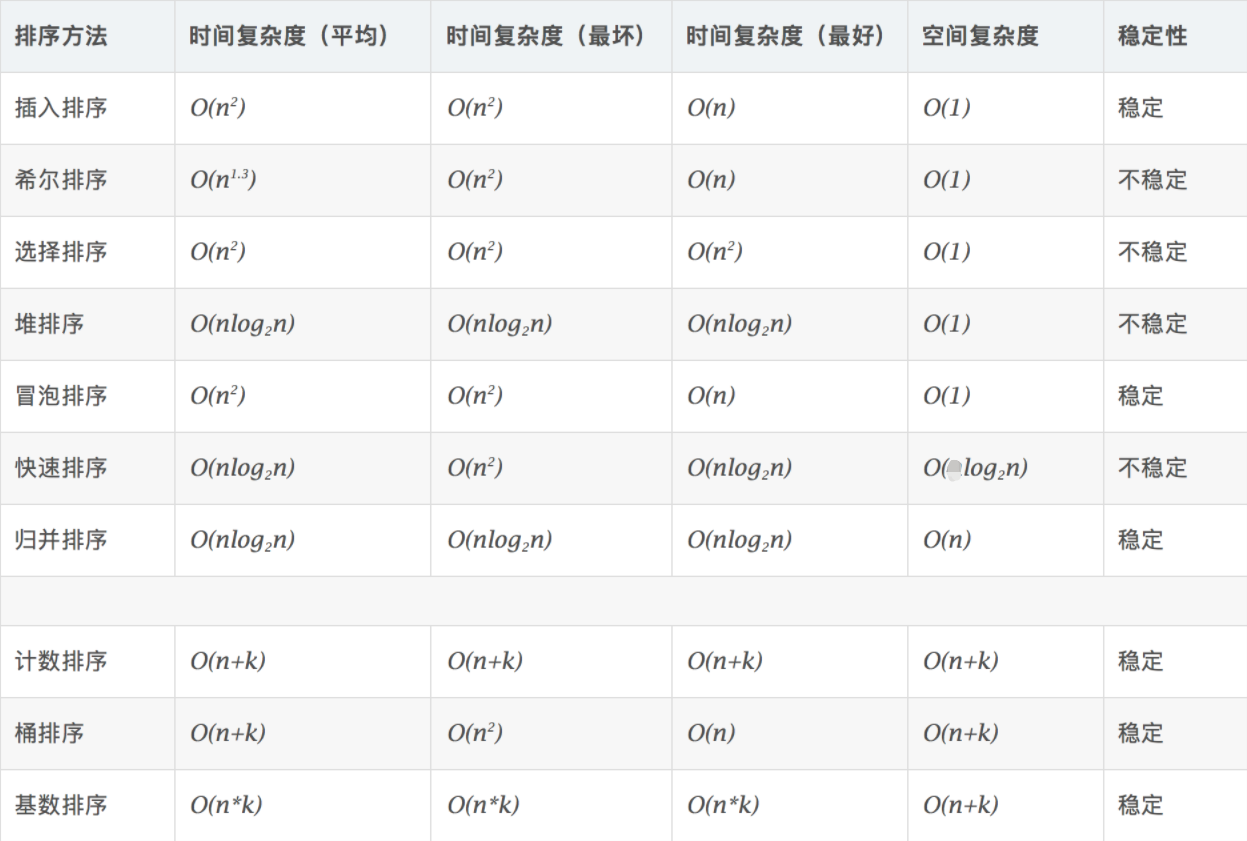
4.1 低效排序
1、冒泡排序 O(n²)

2、选择排序
3、插入排序
4.2 高效排序
1、快速排序原理&快速排序代码 O(nlong n)
缺点:
1、递归会消耗大量的内存资源
2、会出现最坏情况(当列表为倒序时会达到递归深度)
-->解决办法:先随机选一个数出来作为第一个数,打破倒序随机化
2、堆排序前传树的基础知识

- 根节点:有叶子节点的节点
- 叶子节点:没有叶子节点的节点
- 树的深度(高度):从根节点到叶子节点的节点个数,树的深度为4
- 树的度:节点的分支数,eg:A的度为6
- 孩子节点、父节点:D是H的父节点,H是D的孩子节点
- 子树:以E为根节点的树是A的一棵子树
2.1 堆排序前传二叉树的基础知识
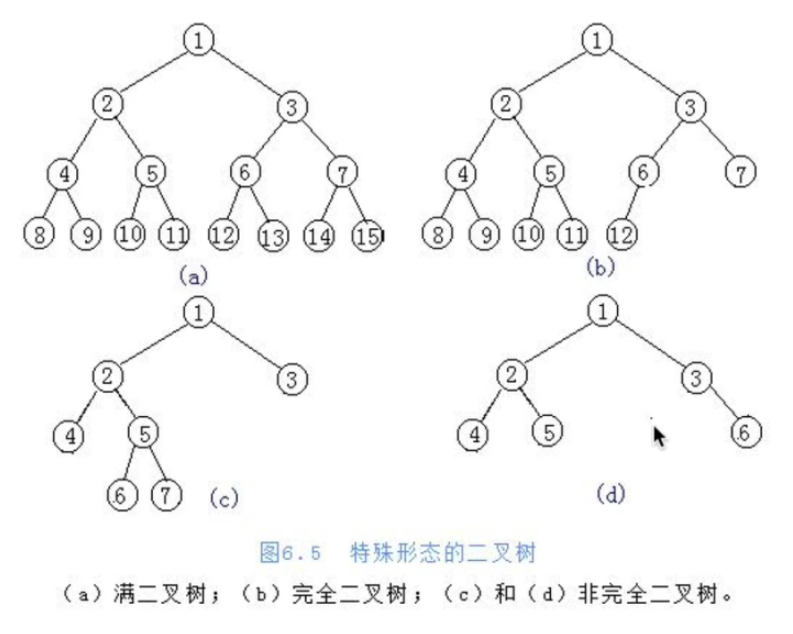
二叉树的存储方式
- 链式存储方式:使用列表存储二叉树
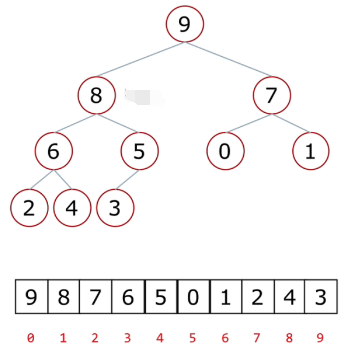
对于完全二叉树父节点下标编号为:i,则左孩子下标编号为2i+1,右孩子下标编号为2i+2
- 顺序存储方式
2.2 堆&堆的向下调整
- 堆就是一种特殊的完全二叉树
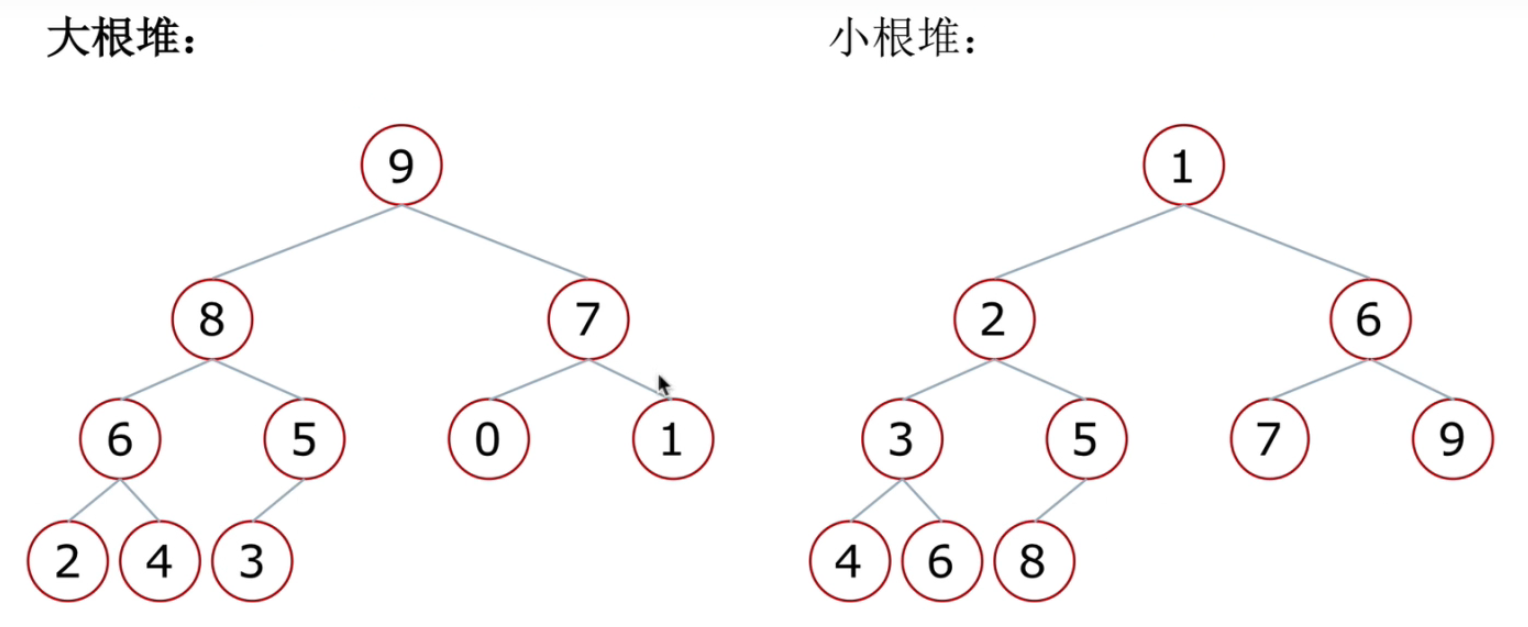
- 大根堆:—棵完全二叉树,满足任一节点都比其孩子节点大
- 小根堆:—棵完全二叉树,满足任一节点都比其孩子节点小
堆的向下调整
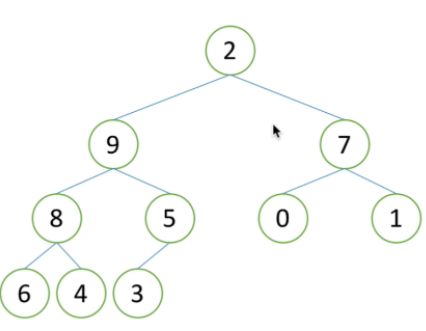
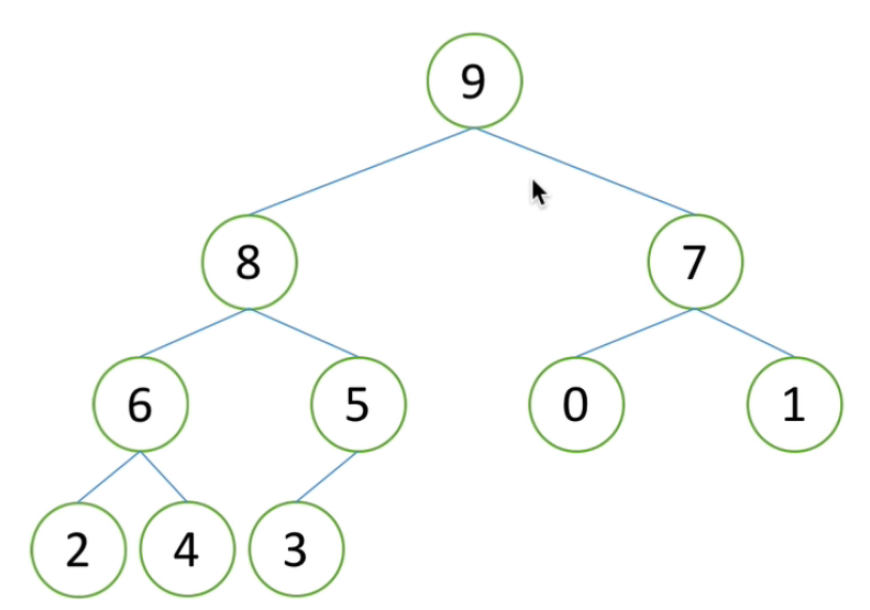
节点的左右子树都是堆,但自身不是堆。以9为根节点和以7为根节点的左右两个树都是大根堆,但是以2为节点的树不是堆,因此要将树向下调整,使其成为一个堆。(每次将其子节点中较大的那个上移,直到成为堆为止)
2.3 堆排序的过程演示
2.4 向下调整函数的实现
2.5 堆排序的实现(1)
2.6 堆排序的实现(2)
2.7 堆排序的时间复杂度
2.8 堆的内置模块
29、topk问题
30、topk实现
32、归并排序归并
31、归并排序实现
33、归并排序复杂度讨论
34、NB三人组小结










