排列组合_均匀分组和部分均匀分组的计算与示例

文章目录

• ​​均匀分组​​

• ​​乘法原理​​

• ​​局部均匀分组​​

• ​​例题​​

理解均匀分组中的去重复计算问题,可以这样入手

均匀分组

为了不引起混淆,以给一批游工人组队(不考虑分配任务,仅仅考虑人员组合可能的情况的种数)作为问题场景

从最简单的均匀分组来看:

(没有第1组和第2组这样组别区分,只有单个分组内的人员构成作(成员间要做区分)为组与组的区别)

• 两个人,均分成两个组,有几种不同分法?

显然,只有一种分法(两个组都是一组一个人)

• 三个人,均分成三组,有几种不同分法?

显然还是只有一种分法(每组一个人这一种分组方法)

利用组合数和分步乘法原理,不考虑去重(保留分组顺序),那么两个问题的解分别表示为

为第一个组选择并分配一个人;在为第二组人选择并分配一个人;…

问题是,如何理解这个结果?

• 其实上述做法是​​考虑组别之间顺序情况下​​的很自然的做法
• 如果需要得到无序别的结果数,只需要做去序操作

​​binomial 美: [baɪˈnoʊmiəl] adj. 【数】二项(式)的​​ 我们不妨对第二个问题进行有顺序区分下的枚举:

abc
acb
bac
bca
cab
cba

共有六种,这正好是排列数的结果,换句话说,就是对均分后的组数(三组),对三个组对象求全排列的结果

• 事实上,组合数之间做乘法,就已经蕴含着顺序;(单个组合数内是无序的)

乘法原理

做一件事，完成它需要分成n个步骤，做第一 步有种不同的方法，做第二步有种不同的方法，……，做第n步有种不同的方法。那么完成这件事共有 N=… 种不同的方法

做完一整件事的若干​​步骤​​中,各个步骤各自存在的方案总数的计算不能脱离步骤间的执行顺序

• 在​​组合数​​​公式的展开中,其分母比对应的​​排列数​​的展开式要多上一部分(可以理解为该部分就是用以去重(去序)的.
• 任意排列数/组合数公式
  

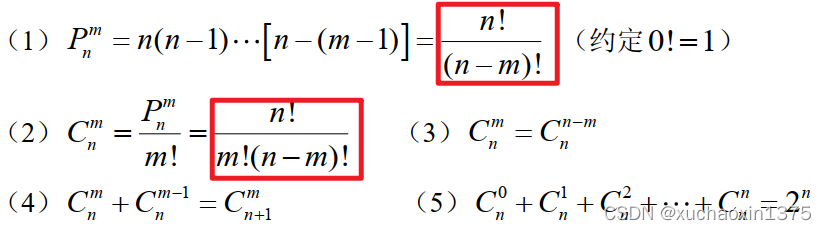
全排列公式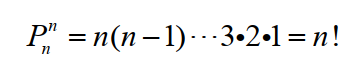

局部均匀分组

例题

人数不等的组别不计入均匀分组的去重计算,例如

解: