文章目录
- 01背包
- 完整代码
- 滚动数组优化:01背包
- 完整代码
上节回顾:
动态规划(3)最大方案数问题
01背包
问题引入:
有n个物品,每个物品的重量分别是 weight[i],每个物品的价值分别是 value[i]。你有一个背包,这个背包共有w 容量,请问你要怎么分配物品,才能使得背包中的物品总价值最高呢?
重量 | 价值 | |
物品0 | 1 | 15 |
物品1 | 3 | 20 |
物品2 | 4 | 30 |
你的背包的容量: 6
这道题是典型的01背包问题,当然你也可以使用暴力来解决这个问题。
即使用回溯法,依次把每一个物品放入背包中,然后依次计算它的最大值,不过这样的方法的时间复杂度将会非常高,所以我们使用动态规划的思想来解决这个问题,而动态规划的具体实现方法则是01背包问题。
解决动态规划问题的五个步骤:
- 确定dp数组以及其下标的含义。
- 确定递推公式
- dp数组的初始化
- dp数组的遍历顺序
- 图例推导dp过程
首先我们以这道题为例:
- 确定dp数组以及其下标的含义
我们创建dp[i][j]二维数组,i 表示dp二维数组的行,表示物品的编号(从0开始);j 表示dp二维数组的列,表示背包容量为 j 时,所能装下的最大价值。
i : 物品编号,表示物品 i
j : 背包的当前容量,当前容量为 j
dp[i][j] :把 编号为 i 的物品放入 容量为 j 的背包,其所能容纳的物品的最大价值是dp[i][j]。
- 确定递推公式
把物品放入背包,我们有两种方案:
- 不放入背包
- 放入背包
什么时候不能把物品放入背包呢?
如果我们之前已经把某一个物品放入了背包,假设之前的物品的容量(我们定为编号i -1)是3,而我们的背包容量是4,而当前的物品(编号 i )的容量是2,显然我们无法把当前的编号为 i 的物品放入背包,因为我们的背包总容量不够,所以,我们无法放入这个物品到背包中,此时我们的递推公式为: dp[i][j]=dp[i-1][j]
简单来说:当前容量为 j 的背包无法容量 编号i的物品,所以此时的dp[i][j] 仍然等于上一次的背包存储的物品的价值dp[i-1][j]。
什么时候要把物品放入背包呢?
首先我们的背包容量 j 必须大于即将放的这个物品的重量,即 j >weight[i],我们可以放入物品 i 到这个背包。dp[i-1][j-weight[i]] 为我们的背包容量为 i-weight[i] 时,不放物品 i 时的最大价值(等同于不放入背包的递推公式)。在这个时候,我们又放入了物品i,因此此时放入了物品i 的背包的最大价值:dp[i-1][j-weight[i]]+value[i]。
综上我们的递推公式:
dp[i][j]=max(dp[i-1][j] , dp[i-1][j-weight[i]]+value[i])
提示:关于为什么要加max ,原因是:
- 你放入了编号 i 物品,那么物品放入后使得当前的背包价值最大呢?
- 还是不放入这个物品,而之前放入的物品(i-1)保持不动,使得背包的价值最大呢?
两者取一个最大值即可算出当前背包容量为 j 时的最佳方案,即局部最优解。
- dp数组如何初始化
由于dp数组中使用了 i -1 等需要以前的计算结果的过程,所以我们必须对dp数组进行初始化。
由于dp数组是一个二维数组,所以我们有必要对第一行与第一列进行初始化,以防万一。
- 第一列的初始化 dp[i][0]:物品的编号为 i,背包的当前容量是0,所以无论是哪个物品,一定放不进背包,所以: dp[i][0]=0
- 第一行的初始化 dp[0][j]:物品的编号为 0(第一个物品),背包的当前容量 j (j>=1),所以一定能放入物品编号为0的物品,因此dp[0][j]=value[0]。
//第一列的初始化
for (int i=0;i<物品的总数;i++)
{
dp[i][0]=0;
}
//第一行的初始化
for (int j=weight[0];j<=w;j++)
{
dp[0][j]=value[0];
}

- dp数组的遍历顺序
根据我们的递推公式:dp[i][j]=max(dp[i-1][j] , dp[i-1][j-weight[i]]+value[i])
因此我们需要首先得到dp[i-1][j] 和dp[i-1][j-weight[i]]的值,而这两个值在二维数组中位于我们的(i,j)的左上方(正上方),所以我们必须从上方和左边开始往下边和右边进行遍历,依次填充。
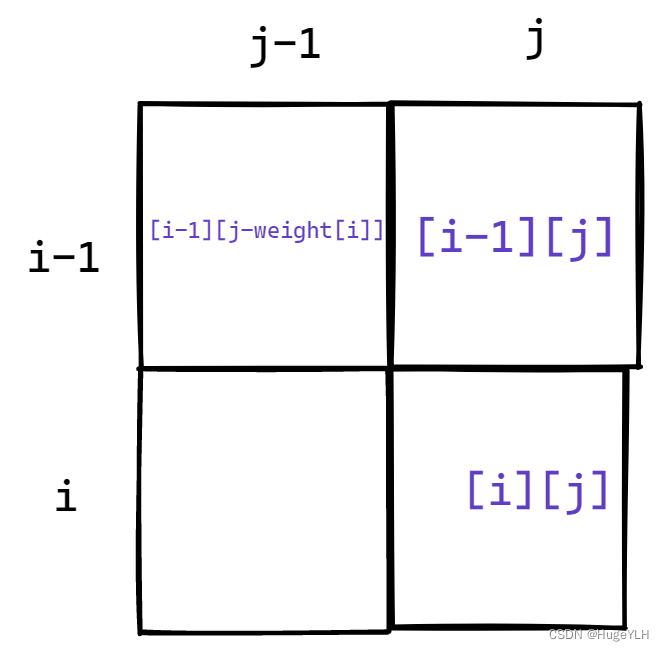
01背包具有两种遍历和填充的方式:
- 首先遍历物品,然后遍历背包容量
- 首先遍历背包容量,然后遍历物品
这里给出两种方式:
num:物品的数量
- 首先遍历物品,然后遍历背包容量:
for (int i=1;i<num;i++)
{
for (int j=0;j<w;j++)
{
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
首先遍历每一行,然后再填充行中的每一列,注意经过之前的初始化,我们的 i 只需要从1开始就行了,i =0 就是第一行的初始化,已经放入我们的背包中了。
- 首先遍历背包容量,然后遍历物品
for (int j=0;j<=w;j++)
{
for (int i=1;i<num;i++)
{
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
首先遍历每一列,然后再填充列中的每一行,同理 i 从1开始即可,这两种方案都是一致的。
因为递推公式是一致的。
- 图例推导dp数组
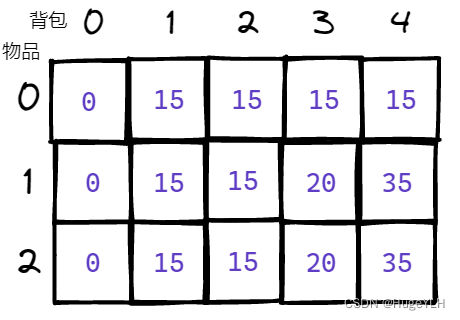
完整代码
//二维dp数组
void bag_question()
{
//物品的重量与价值
vector<int> weight{ 1,3,4 };
vector<int> value{ 15,20,30 };
int num = weight.size();
//背包的容量(大于等于物品的最大容量,否则就无法放下这个物品)
int bagweight = 4;
//创建二维dp背包数组:dp[i][j] i:编号i的物品 0-1-2 j:背包的容量j 0-1-2-3-4-5-6
//这是一个 3x7 的二维数组
vector<vector<int>> dp(num, vector<int>(4 + 1));
int m = dp.size();
int n = dp[0].size();
//dp数组的初始化
//1. 第一列: j=0,背包的容量为0,无法放任何物品
for (int i = 0; i < m; i++)
{
dp[i][0] = 0;
}
//1. 第一行: i=0,背包的容量>=1,一定可以放下第一个物品(编号0),保存其价值
for (int j = weight[0]; j <= bagweight; j++)
{
dp[0][j] = value[0];
}
#if 0
//先遍历物品,再遍历背包,跳过编号0的物品
for (int i = 1; i < num; i++)
{
for (int j = 0; j <= bagweight; j++)
{
//背包无法容纳这个物品: dp[i][j]=dp[i-1][j]
if (j<weight[i])
{
dp[i][j] = dp[i - 1][j];
}
//背包可以容纳这个物品:dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[0]]+value);
else
{
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
#else
//先遍历背包,再遍历物品,跳过容量0的背包容量
for (int j = 0; j <= bagweight; j++)
{
for (int i = 1; i < num; i++)
{
if (j < weight[i])
{
dp[i][j] = dp[i - 1][j];
}
else
{
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
#endif
for (auto& x : dp)
{
for (auto& y : x)
{
cout << y << " ";
}
cout << endl;
}
cout << dp[num - 1].back() << endl;
}
测试:
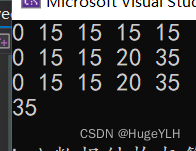
滚动数组优化:01背包
滚动数组:就是把二维dp数组降为一维dp数组。
使用滚动数组的条件:需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
- 确定dp数组及其下标关系
因此,我们完全可以把dp[i][j]:把第i个物品放入背包容量为j时的价值。
优化成dp[j]:背包容量为 j 时的价值。
遇到某个物品仍然有两种选择:
- 要么不放这个物品,还等于其本身: dp[j]=dp[j]
- 要么放这个物品:dp[j]=d[j-weight[i]]+value[i]
- 递推公式的推导
递推公式: dp[j]=max (dp[j] , dp[j-weight[i]] + value[i])
- dp数组的初始化
初始化: dp[0]=0
- dp数组的遍历
一维dp与二维dp的不同之处:
二维dp的写法中,遍历背包的顺序是不一样的!
一维dp的遍历:
num是物品的总数,w是背包的总容量
for (int i=0;i<num;i++)
{
for (int j=w;j>=weight[i];j--)
{
dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
}
}
可以发现我们遍历背包重量的时候是逆序的!
为什么呢? 举一个例子: 如果是正序;
物品重量:10 ,价值 20
背包总容量: 20
dp[ 1 ]=dp[ 1-weight[0] ]+value[0] = 20
dp[ 2 ]=dp[2-weight[0] ]+value[0]=20 + 20 =40
进行了两次计算dp[1]的值,因此我们需要采用逆序:
dp[ 2 ]=dp[2-weight[0] ]+value[0]= 20
dp[ 1 ]=dp[ 1-weight[0] ]+value[0] = 20
- 图例推导dp过程:
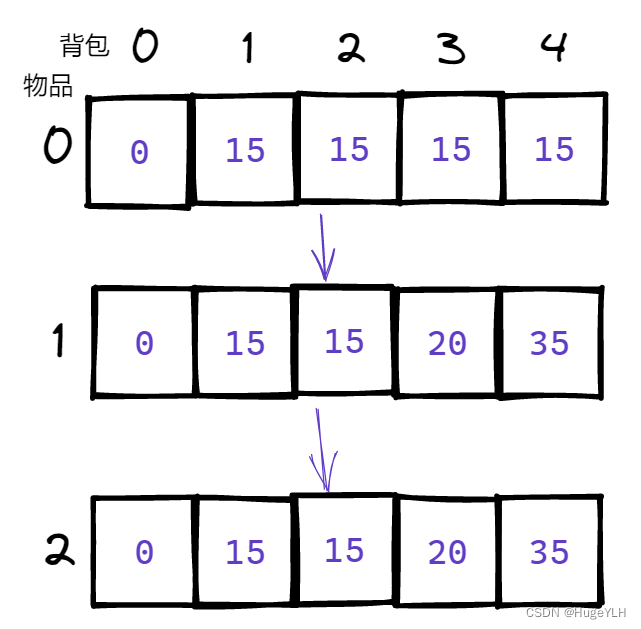
完整代码
//一维dp数组
void bag_question_2()
{
//物品的重量与价值
vector<int> weight{ 1,3,4 };
vector<int> value{ 15,20,30 };
int num = weight.size();
//背包的容量(大于等于物品的最大容量,否则就无法放下这个物品)
int bagweight = 4;
//创建一维dp背包数组
vector<int> dp(bagweight + 1);
int m = dp.size();
//dp数组的初始化
//1. dp[0]表示背包容量为0,无法放任何物品,因此初始化为0
dp[0] = 0;
//先遍历物品,再遍历背包,跳过编号0的物品
for (int i = 0; i < num; i++)
{
for (int j = bagweight; j >= weight[i]; j--)
{
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
for (auto& x : dp)
{
cout << x << " ";
}
cout << endl;
cout << dp.back() << endl;
}










