文章目录

• Receptive Field
• • forward
  • • 第i层和i-2层的关系
    • 第i层和第i-1层的关系
  • backward

Receptive Field

forward

从浅层往深层计算。

示意图说明：

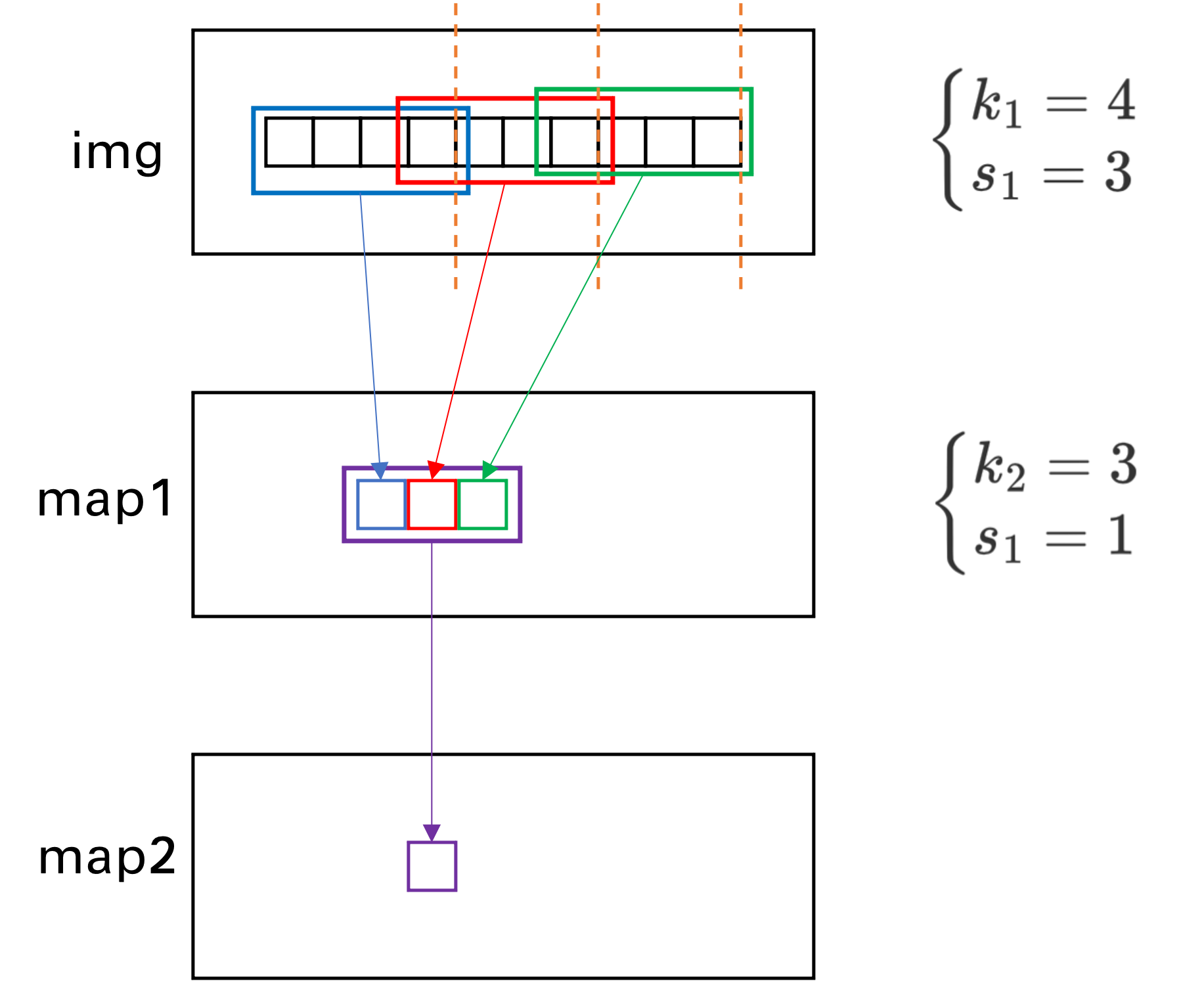
​图中共有三层，图像层img，第一层map1，第二层，map2。为了方便推导，我们使用一维卷积进行演示。一个正方框表示一个像素点，长条状的就是卷积核，为了清楚的分辨出卷积核移动的位置，做了颜色差别处理和长宽放大。箭头所指的是经过这次卷积后产生的图像。

$$\begin{array}{r}first=\{\begin{array}{l}{k}_1=4\\ s_2=3\end{array}\\ second=\{\begin{array}{l}{k}_2=3\\ s_1=1\end{array}\end{array}$$
第一层卷积核fisrt大小为4，步长为3，第二层卷积核second大小为3，步长为1。

符号定义：

$$\begin{array}{rl}& r_i:第i层感受野大小\\ & k_i:第i层卷积核大小\\ & s_i:第i层卷积步长\end{array}$$
规定$r_0=1$表示图像层的感受野大小为1。推导过程中，大家可以自行发挥推导过层，其中我们可以用手动数来验证我们的推导公式是否正确。

$r_1$表示第一层，即map1层。第一层感受野大小为4。显然：
$$r_1=k_1=4$$

$r_2$表示第二层，即map2层。第二层感受野大小为10。显然:
$$r_2\ne k_2=3$$
显然:
$$r_2\ne k_2\ast k_1=12$$
当我们计算第二层$r_2$时，看图！感受野大小与第二层卷积核(k=3) 将 第一层map1中套起来的三个像素有关。可这三个像素在img层中涉及到的像素有重叠的。所以不能直接所不能简单的使卷积核的相乘。

第i层和i-2层的关系

接下来，我将解析如何将感受野与卷积核建立联系，此推导过程可类比于输出图像的计算公式推导。

计算$r_2$肯定要看第二层卷积核在map1上包括的范围。

感受野大小计算公式分解为：首项+其他项

既然上面提到有重叠，那我们利用首项+其他项的思想去重叠。

首项计算：map1中的第一个蓝框作为首项，单独拿出来，它所占的感受野大小为$k_1$。

其他项：map1中第二红框，第三绿框作为其他项。他们在img上的包裹的图像大小为步长$s_1$，(黄色虚线之间)。这样计算是没有重叠的。总共包括的感受野大小为：$(k_2-1)\ast s_1$

综上：
$$r_2=(k_2-1)\ast s_1+k_1$$
此时我们建立了，第$i$层和第$i-2$层的关系。即第二层map2一个方框在图像层img包含的相邻元素的个数。

第三层：
$$r_3=(k_3-1)\ast s_2+k_2$$
重新回顾下，计算第$r_2$在img的相邻元素时，我们要计算第二层卷积核在第一层map1包含相邻元素的个数,此个数就是$k_2$个

此时我们根据上述$r_3$公式，知道了第三层map3在第一层map1中相邻元素的个数。

将$r_3$在map1中的个数替换$r_2$中的个数$k_2$，即可得到第三层map3在img图像上包含的相邻元素的个数。
$$r_3=(((k_3-1)\ast s_2+k_2)-1)\ast s_1+k_1$$

第i层和第i-1层的关系

建立第i层和第i-1层的关系。

联立$r_2,r_3$，消去$k_1$，得到
$$\begin{array}{rl}& \{\begin{array}{l}{r}_2=(k_2-1)\ast s_1+k_1\\ r_3=(((k_3-1)\ast s_2+k_2)-1)\ast s_1+k_1\end{array}\\ ⟹& r_3=(k_3-1)\ast s_2\ast s_1+r_2\end{array}$$

归纳：
$$\{\begin{array}{l}{r}_1=k_1,k=1\\ r_i=(k_i-1)s_i\ast s_{i-1}\ast s_{i-2}\ast \cdots \ast s_1+r_{i-1},k>1\end{array}$$
令$s_0=1,r_0=1$,则：
$$r_i=(k_i-1)\prod _{j=0}^i{s}_j+r_{i-1}$$

backward

从后往前算，待续