文章目录
- 题目描述
- 题解
- 暴力
- 动态规划
- 中心开花
- 马拉车
题目描述
给定一个字符串s,找出s中最长的回文子串
题解
暴力
先想一个最直观最简单的:遍历全部子串,依次判断是否是回文,然后取其中最长的作为答案。
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
int begin = 0, end = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// 当前子串是回文, 且长度大于最大长度, 则更新起点和终点
if (isPalindrome(s, i, j) && j - i > end - begin) {
begin = i;
end = j;
}
}
}
return s.substring(begin, end + 1);
}
// 判断 [l, r] 区间的子串是否是回文串
private boolean isPalindrome(String s, int l, int r) {
while (l < r && s.charAt(l) == s.charAt(r)) {
l++;
r--;
}
return l >= r;
}
}枚举全部子串的复杂度为 ,而判断每个子串是否是回文的复杂度为 ,所以整体的时间复杂度是
判断每个子串是否是回文的复杂度为 ,可以理解为子串的平均长度是 ,而判断回文的复杂度和子串长度是呈线性相关的。
推导:全部子串的个数是:
所有子串的总长度是:
加上
加上
加到 …
结果就是
把分子部分展开,得
得
前半部分根据公式,求得为 ,是 的,用子串总长度()除以子串总数(),得到子串的平均长度是 的。
暴力法的时间复杂度太高,提交会报超时。

动态规划
暴力法的过程中,其实做了很多重复的计算。我们设 来表示子串 是否为回文串,若是,则为true,否则为false。
那么 的取值,只取决于 。所以我们可以利用先前计算过的结果,来减少重复计算。
注意循环的顺序,我们需要确保在计算 时,对于 区间内的所有 都已经计算完毕。
于是,我们按照子串的长度,从小到大递增,来进行循环。
动规的边界条件是,长度为1或2的子串,这些子串的 状态我们可以预处理出来。
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
boolean[][] f = new boolean[n][n];
int begin = 0, end = 0; // 确保至少能取到长度为1的子串
// 预处理长度为1或2的子串
for (int i = 0; i < n; i++) {
f[i][i] = true;
if (i > 0 && s.charAt(i) == s.charAt(i - 1)) {
f[i - 1][i] = true;
begin = i - 1;
end = i;
}
}
// 从大小为3的长度开始枚举
// 不能从2开始枚举, 因为求解[i,i+1]时, 会使用[i+1,i]这样的无效状态
for (int len = 3; len <= n; len++) {
for (int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1;
if (f[i + 1][j - 1] && s.charAt(i) == s.charAt(j)) {
f[i][j] = true;
begin = i;
end = j; // 由于枚举的子串长度是递增的, 则每次更新总是没错的
}
}
}
return s.substring(begin, end + 1);
}
}动规,需要计算的全部状态,也就是全部子串,为,计算每个状态需要 ,所以动规的时间复杂度是
中心开花
动规求解子串的状态是自顶向下的,即从两边往中间缩拢。我们也可以自底向上求解,以每个位置为中心,尝试向左右两边扩散开去,找到以当前位置为中心的最长回文子串。然后将每个位置作为中心能得到的最长子串,再取一个最值即可。
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
int begin = 0, end = 0;
for (int i = 0; i < n; i++) {
// 注意需要处理回文串为奇数和为偶数的情况
int len = expand(s, i, i + 1); // 偶数
if (2 * len > end - begin + 1) {
begin = i - len + 1;
end = i + len;
}
len = expand(s, i - 1, i + 1); // 奇数
if (2 * len + 1 > end - begin + 1) {
begin = i - len;
end = i + len;
}
}
return s.substring(begin, end + 1);
}
// return 向两边扩散的最长半径
private int expand(String s, int l, int r) {
while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)) {
l--;
r++;
}
// 若是偶数回文串, 如 abba, 则返回2
// 若是奇数回文串, 如 abcba, 则返回2
return (r - l - 1) / 2;
}
}
中心开花的时间复杂度也是 ,枚举每个位置作为中心,复杂度为,对每个位置往两边扩散,复杂度也为,所以总的时间复杂度是。
然而中心开花的方法,比动态规划要快,因为这种方式省掉了一些不可能作为答案的子串的状态计算。比如以i为中心,向两边扩散,当扩散到半径为2时,发现已经不是回文了,则对于以i为中心,半径大于2的那些子串,不需要再做计算了。也就是说它少计算了一些子串的状态。而动态规划是把所有子串都计算了一遍。
马拉车
Manacher算法,是在中心开花法上面的优化,能够将时间复杂度降低为线性的。它主要是利用了先前计算的结果,通过回文镜像对称的特点,来减少重复的状态判断。具体思路如下:
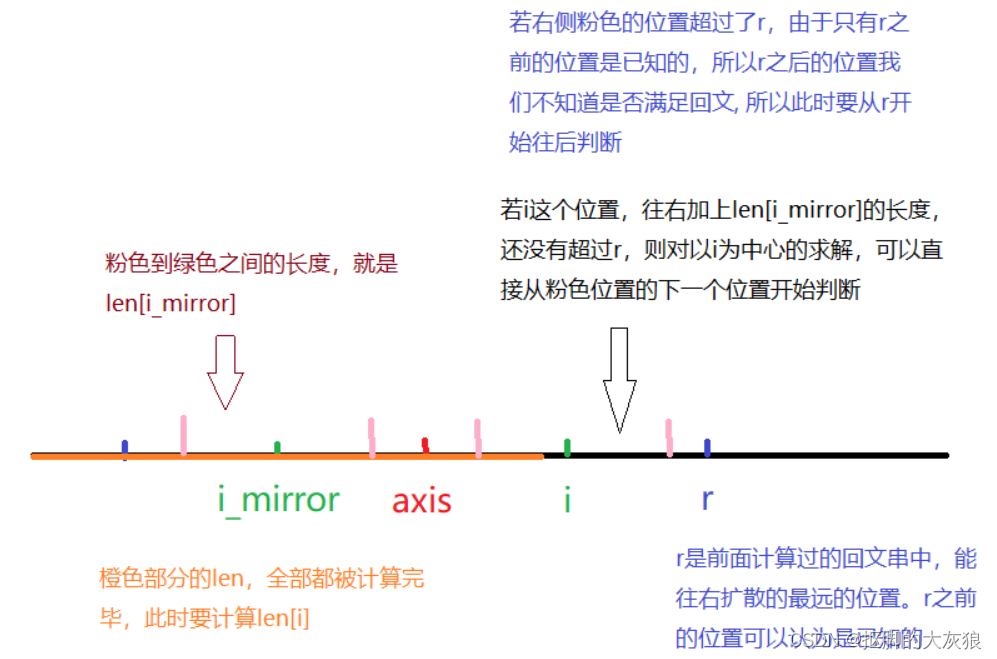
我们先只考虑回文串为奇数长度的情况。我们从左往右枚举每个位置作为中心点时,都能够得到以这个点为中心,最大的回文子串。我们将以i为中心,往两边扩散,能够达到的最远的半径,记为臂长len[i]。
比如字符串 abcocnpncoccd,下标为6的位置是p,其往两边扩散,能达到的最长半径为4(我们只考虑回文串长度为奇数,且中心点不纳入半径计算),即以p为中心的最长回文子串是cocnpncoc,则len[6] = 4。则以下标6为中心的回文子串,其扩散出来,能够覆盖到下标10(6+4)。假设对于下标小于6为中心,扩散出来的回文子串,都没法达到下标10的位置,则我们称10为此时能够覆盖到的最远的位置,记为r。
当我们对于i > 6,需要计算len[i]时,可以利用前面的结果。当r > i时,说明位置i已经被之前的某个中心点的最长回文子串所覆盖。假设我们此时要计算的是位置9,即i = 9。此时r = 10,且这个r是由中心点6所维护,我们设维护r的中心点的下标为axis。
由于以axis为中心的最长回文子串,覆盖了i这个位置,且回文具有对称的特性。那么我们可以找到i关于axis对称的位置,称其为i_mirror。容易得知i_mirror = 2 * axis - i。计算的过程可以这样想,假设axis到i的距离是x,则axis + x = i,那么对称点i_mirror = axis - x,将两式相加,得2 * axis = i + i_mirror。
由于i_mirror位于axis之前,则len[i_mirror]已经是被计算过的。
马拉车的核心思想就是利用这个len[i_mirror]。
上面考虑的只是对于回文串长度为奇数这一种情况。对于偶数,我们可以先将其变成奇数。方法是,在每个字符之间插入一个符号(随便什么符号皆可,不会影响原有字符的回文判断),假设加入#。
#b#c#b#b#d#b#,则原来的奇数长度的回文串,如bcb,仍然是奇数长度回文串,#b#c#b#。
原来的偶数长度的回文串,如bb,变成了奇数长度回文串,#b#b#。
写成代码如下
class Solution {
public String longestPalindrome(String s) {
// 添加分隔符, 转化为奇数长度的字符串
StringBuilder sb = new StringBuilder("#");
for (int i = 0; i < s.length(); i++) {
sb.append(s.charAt(i)).append("#");
}
s = sb.toString();
int n = s.length();
int[] len = new int[n]; // 以每个点为中心, 能够扩展出来的最长半径
int axis = -1, r = -1; // r是回文串能覆盖到的最远的右端点, axis是对应的中心
int max_len = 0, max_axis = 0; // 记录答案
for (int i = 0; i < n; i++) {
int i_len = 0;
if (r > i) { // 当i被r覆盖住
int i_mirror = 2 * axis - i;
int i_min_len = Math.min(r - i, len[i_mirror]); // i 的最小半径
i_len = expand(s, i - i_min_len - 1, i + i_min_len + 1); // 从最小半径往外扩散
} else { // 否则按照朴素的中心开花进行扩散
i_len = expand(s, i - 1, i + 1);
}
if (i + i_len > r) {
// 更新 r 和 axis
r = i + i_len;
axis = i;
}
len[i] = i_len;
if (i_len > max_len) {
// 更新答案
max_len = i_len;
max_axis = i;
}
}
// 还原, 得到结果
int begin = max_axis - max_len, end = max_axis + max_len;
StringBuilder res = new StringBuilder();
for (int i = begin; i <= end; i++) {
if (s.charAt(i) != '#') res.append(s.charAt(i));
}
return res.toString();
}
private int expand(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
left--;
right++;
}
return (right - left - 2) / 2;
}
}
上面的描述其实不是特别准确。准确说,当我们需要计算len[i]时,有3种情况
-
i + len[i_mirror] < r,此时len[i]其实不用算了,len[i]就等于len[i_mirror] -
i + len[i_mirror] > r,此时len[i]也不用算了,len[i]就等于r - i (最远的回文扩散到r) -
i + len[i_mirror] = r,此时才需要计算,右侧端点从r + 1的位置,左侧端点从对应位置,开始往两边扩散
所以,这里就能看到马拉车算法的优秀之处了。只要r足够大,能够覆盖到足够远的位置,则覆盖范围内的i的计算,很多时候都可以不劳而获,仅仅在i + len[i_mirror] = r时,才需要往两边扩散。而往两边扩散,又使得r会被更大的值更新。
这样写成代码应该如下(只改动了r > i这个分支下面的部分)
class Solution {
public String longestPalindrome(String s) {
// 添加分隔符, 转化为奇数长度的字符串
StringBuilder sb = new StringBuilder("#");
for (int i = 0; i < s.length(); i++) {
sb.append(s.charAt(i)).append("#");
}
s = sb.toString();
int n = s.length();
int[] len = new int[n]; // 以每个点为中心, 能够扩展出来的最长半径
int axis = -1, r = -1; // r是回文串能覆盖到的最远的右端点, axis是对应的中心
int max_len = 0, max_axis = 0; // 记录答案
for (int i = 0; i < n; i++) {
int i_len = 0;
if (r > i) { // 当i被r覆盖住
int i_mirror = 2 * axis - i;
if (i + len[i_mirror] < r) i_len = len[i_mirror];
else if (i + len[i_mirror] > r) i_len = r - i;
else {
int i_min_len = len[i_mirror];
i_len = expand(s, i - i_min_len - 1, i + i_min_len + 1);
}
} else { // 否则按照朴素的中心开花进行扩散
i_len = expand(s, i - 1, i + 1);
}
if (i + i_len > r) {
// 更新 r 和 axis
r = i + i_len;
axis = i;
}
len[i] = i_len;
if (i_len > max_len) {
// 更新答案
max_len = i_len;
max_axis = i;
}
}
// 还原, 得到结果
int begin = max_axis - max_len, end = max_axis + max_len;
StringBuilder res = new StringBuilder();
for (int i = begin; i <= end; i++) {
if (s.charAt(i) != '#') res.append(s.charAt(i));
}
return res.toString();
}
private int expand(String s, int left, int right) {
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
left--;
right++;
}
return (right - left - 2) / 2;
}
}
其实效果相差不大,在前面那种写法下,在<或者>时,只会多进行了一次比较,但前面的写法更简洁一些。
马拉车的时间复杂度为,可以理解为每个位置的字符最多会被比较一次。
参考详解马拉车算法——原理、实现与练习
