
Ⅰ. 前置知识:最大小项、布尔方程
0x00 卡诺图的定义
📚 定义:布尔方程


- letter :一个常数或一个变量
- literal : 一个字母或其补码
eg.

0x01 乘积项与合项(Product and Sum term)
乘积项(Product term):
Product term (product, term)
1
a non-constant literal
a conjunction of non-constant literals where no letter appears
more than once

例如:

,本算式中,

就是一个乘积项
合项(Sum term):
Sum term
0
a non-constant literal
a disjunction of non-constant literals where no letter appears
more than once

0x02 最小项与最大项(Minterm and Maxterm)
📚 最小项的定义:

个变量

的最小项是

个因子的乘积。
一个函数的某个乘积项包含了函数的全部变量,
其中 每个变量 都以它的 原变量 或 反变量的形式 在乘积中出现,且 仅出现一次。
我们称这个乘积项为该函数的一个标准积项 —— 最小项 (Minterm) 。
简单来说,最小项就是所有变量从头到尾只用一次的乘积项 (product term),比如变量

:

我们通常用小写字母

来表示最小项,这里的

为下标,其确定方式如下:将最小项中的原变量记为 1,非变量记为 0,当变量顺序确定后,可以按顺序排列成一个二进制数,与这个二进制数相对应的十进制数就是该最小项的下标

。

若将原变量记为 1,反变量记录 0,则对应十进制后的值则为

的表示方式:

既然下标

已经确认,我们就可以将

记为:

📚 最大项的定义:
对于一个

变量的函数,该和项包括

个变量中的每一个变量。
一个函数的某个和项包含了函数的全部变量,
若 每个变量 都以 原变量 或 反变量的形式 出现一次,且 仅出现一次,
我们称这个求和项为该函数的一个标准和项 —— 最大项 (Maxterm) 。
所有变量从头到尾只用一次的合项 (sum term),称为最大项。比如变量

:

我们通常用大写字母

来表示最大项,最大项下标

确定方式与最小项下标的取值恰好相反。
若将原变量记为 0,反变量记录 1(与最小项相反),三个变量形成的八个最大项记为:

(这里采用了 "拔" 的写法,这也是可以的,某些教材是采用 ' 表示的,只是表示方法不同)
🔍 参照表: 

0x03 布尔方程式(Boolean function)
- 积之合 (Sum of product) ,简写为 ,用符号 表示。
- 析取范式 (disjunctive normal form) ,简写为 ,用符号 表示。

- 和之积 (Product of sum) ,简写为 ,用符号 表示。
- 合取范式 (conjunctive normal form) ,简写为 ,用符号 表示。

- 积之合的典范:极小项之和 (Canonical sum of product : sum of minterms) :

- 合之积的典范:极大项之和 (Canonical product of sum : product of maxterms)

Ⅱ. 卡诺图(K-Map)
0x00 卡诺图介绍(Karnaugh Map1953.NOV)
卡诺图 是一种平面方格图,每个小方格代表逻辑函数的一个最小项,故又称为最小项方格图。 方格图中相邻两个方格的两组变量取值相比,只有一个变量的取值发生变化,按照这一原则得出的方格图(全部方格构成正方形或长方形)就称为卡诺方格图,简称卡诺图。
卡诺图是一种描述逻辑函数的特殊方格图。
每一个方格代表逻辑函数的一个最小项,且几何相邻的小方格具有逻辑相邻性。
即 两相邻的小方格所代表的最小项只有一个变量取值不同。
对于有

个变量的逻辑函数,其最小项有

个。因此该逻辑函数的卡诺图是由

个小方格构成的,每个小方格都满足逻辑相邻项的要求。
几何相邻:在几何位置上,上下左右或左右相邻
逻辑相邻:两个最小项,只有一个变量的形式不同,其余的都相同。逻辑相邻的最小项可以合并。
📚 在布尔逻辑的积项和式中:
若
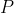
蕴涵

,则乘积项
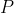
是布尔函数

的涵项(implicant)。更加准确的说:
- 是 个变量的布尔函数
- 是乘积项(Product term)
- 若对于使 得到值 1 的所有组合, 也等于 1,则 蕴涵 ( 是 的涵项)
这意味着在布尔空间的自然次序上
,比如函数:

蕴涵自

和很多其他的项: 它们是

的 涵项。

蕴含项(Implicant):

个 1 的蕴含。

威拉德·冯·奥曼·蒯因 做过如下定义:

- 不包括在更大的蕴含(Implicant)中的蕴含。
- 为最少化文字数量的涵项,即如果从 P 去除任何 "文字"(literal)都导致 成为 的非涵项。
- 例如 100 和 101 是某逻辑函数的两个涵项,那么 10x 就是函数的一个质涵项,其中的 1 和 0 两个数字不可再去掉。
基本质涵项(essential prime implicant):
- 在形成一个 prime Implicant 的 1 中,至少有一个不属于另一个 Implicant,而是属于自己的 Prime Implicant 捆绑包的 Prime Implicant。
- 蕴涵于不满足任何其他质涵项的最小项 (minterm) 的那些质涵项——若存在只被一个质涵项覆盖的最小项,则覆盖该最小项的质涵项为基本质涵项。
- 如果以卡诺图的形式来描述逻辑函数,可以发现只有一种方式可以圈选这个输入组合。

简化函数:包括全部

,和一部分非必要的(non-essential)

蕴含项(Implicant):一个包含在函数
中的乘积项

首要隐含子(PI):
- 一个不包括在 的任何其他蕴含中的蕴含(不能与另一个项结合以消除一个变量)

- 指包括一个不包括在任何其他 中的最小项的
⚡ 优化算法(Optimization Algorithm)
找到所有的质含项(prime implicants)
在解决方案中包括所有必要质涵项(Essential Prime Implicant)
选择一个最小成本的 非基本质涵项集合(set of non-essential prime implicants),以覆盖所有尚未覆盖的最小项(minterms)
0x01 卡诺图(Karnaugh Map)

0x02 变量图(variable map)

💭 变量图的例子:

0x03 三变量图(Three-variable Maps)

💬 观察:三变量和四变量地图上的相邻关系(Adjacencies on three- and four-variable maps)


0x04 进位与求和函数的地图表示(Map representation of carry and sum func)

💭 举个例子:


具有两个最小形式的函数的例子(Example Function with Two Minimal Forms):

0x05 四变量图(Four-variable Maps)





💭 卡诺图的例子:


0x06 五变量图(A Five Veriable Map)
一张五变量地图由25=32个方块组成:

0x07 卡诺图无关项(K-map with Don’t Cares)
在数字逻辑中,函数的无关术语是输入序列,对于该序列,函数输出无关紧要。已知永远不会发生的输入是不可实现的术语。这两种类型的条件在逻辑设计中都以相同的方式处理,为简洁起见,可以统称为无关条件。实现该功能的逻辑电路的设计人员无需关心此类输入,但通常可以随意选择电路的输出,以生成最简单的电路。
有时,一个 function table 或 map 会存在一些并没有什么卵用的项目:
- 极小项(Minterm)的输入值永远不会出现
- 或者,极小项(Minterm)的输出值根本用不着
在这些情况下,我们不需要定义其输出值,因为根本就没有这个必要!
我们可以将这些输出值被定义为 "无关项",即 Don’t cares
通过在函数表或映射中放置 " 无关条件的 "(加入一个 x ),就能降低逻辑电路的成本。
💭 举个例子:
- 一个逻辑函数的输入是
- 数字的二进制代码。只有 0 到 9 的代码被使用。1010 到 1111 这六串代码(10~15)从未出现过,可以将这些代码的输出值设为 x ,代表无关项。

🔺 下列红色表示的部分即为无关项 Don't cares :
- 不完全指定函数的极小项展开(Minterm expansion for incompletely specified function)
- 不完全指定函数的极大项展开(Maxterm expansion for incompletely specified function)
极小项解:
(在极小项中不使用)

0x08 七段式显示器(A seven-segment display)

其真值表如下(Truth table of seven segment display):

📌 [ 笔者 ] 王亦优
📃 [ 更新 ] 2022.
❌ [ 勘误 ] /* 暂无 */
📜 [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,
本人也很想知道这些错误,恳望读者批评指正!
📜 参考资料 Introduction to Logic and Computer Design. International edition, 2008 Alan B.Marcovitx McGraw-Hill Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/. 卡诺图化简法_Samplay的博客_卡诺图 |

