Jenkins教程-20-常用插件-Parameterized Trigger

51. N-Queens

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens’ placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Example 1:

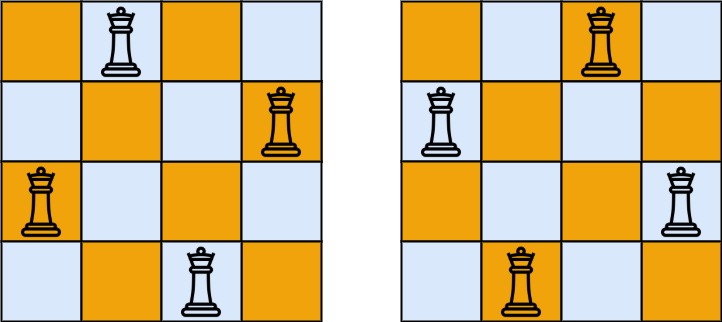
**Input:** n = 4
**Output:** [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
**Explanation:** There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

**Input:** n = 1
**Output:** [["Q"]]

Constraints:

• 1 <= n <= 9

JavaScript Solution

/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function(n) {
    let col = Array(n).fill(0)
    let pie = na = new Array(2*n - 1).fill(0)
    let board = []
    let res = []
    for(let i=0; i< n; i++){
        board.push(Array(n).fill('.'))
    }
    return dfs(0,n,col,pie,na,board,res),res
};

let dfs = (row, n, col, pie, na, board, res)=>{
    if(row==n){
        let rows =[]
        for(let i=0;i<n;i++){
            rows.push(board[i].join(''))
        }
        res.push(rows)
        return
    }
    for(let i=0; i < n; i++){
        if(!col[i] && !pie[row + i] && !na[row - i + n - 1] ){
            [ col[i], pie[row + i], na[row - i + n - 1] ] = [1,1,1]
            board[row][i] = 'Q'
            dfs(row + 1, n, col, pie, na, board, res)
            board[row][i] = '.'
            [ col[i], pie[row + i], na[row - i + n - 1] ] = [0,0,0]
        }
    }
    return 
}