leetcode 105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

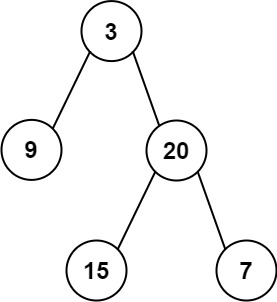
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000

• inorder.length == preorder.length

• -3000 <= preorder[i], inorder[i] <= 3000

• preorder 和 inorder 均 无重复 元素

• inorder 均出现在 preorder

• preorder 保证 为二叉树的前序遍历序列

• inorder 保证 为二叉树的中序遍历序列

Related Topics

树

数组

哈希表

分治

二叉树

思路1：递归

根据先序和中序的特点：创建一个根据先序和中序遍历恢复一棵树的方法。

假设先序在数组的下标范围是[i,j]，初始是[0,length-1]，同理，中序是[x,y]

• 首先，先序遍历的第一个元素就是根节点，再中序遍历中找到这个值的位置mid。

• 中序遍历左子树下标的范围是[x,mid-1]，右子树下标范围是[mid+1,y]。

• 由中序遍历根节点位置可知，左子树中有mid-x个元素，在先序遍历中，左子树第一个元素的下标是i+1，那么第mid-x元素的下标是i+mid-x,那么左子树的范围是[i+1,i+mid-x]，右子树的范围是[i+mid-x+1,y]

左子树和右子树同样也是一棵树，可以继续使用这个方法递归。

当先序或者中序的下标范围越界时，就结束。

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTree(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
    }
    //i，j是先序的范围  x，y是中序的范围
    public TreeNode buildTree(int[] preorder,int i,int j,int[] inorder,int x,int y){
        if(j < i){
            return null;
        }
        //先序的第一个节点是一棵树的根节点
        TreeNode p = new TreeNode(preorder[i]);
        //找到根节点在中序的位置mid
        int mid = 0;
        for(mid = x; mid <= y;mid++){
            if(inorder[mid] == preorder[i]){
                break;
            }
        }
        //对于中序而言，[x,mid-1]是左子树元素 [mid+1,y]是右子树元素
        //对于先序而言，左子树中元素个数是mid-x,左子树第一个元素下标是i+1,总共mid-x个元素，下标范围是[i+1,i+mid-x]
        //右子树的范围是[i+mid-x+1,j]
        p.left = buildTree(preorder,i+1,i+mid-x,inorder,x,mid-1);
        p.right = buildTree(preorder,i+mid-x+1,j,inorder,mid+1,y);
        return p;
    }
}
    执行耗时:3 ms,击败了55.59% 的Java用户
            内存消耗:41.2 MB,击败了18.03% 的Java用户
            

参考leetcode官方：可以提前把中序序列放到哈希表中，这样查根节点的位置就可以以O(1)的时间复杂度。

class Solution {
​
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        HashMap<Integer,Integer> map = new HashMap<>();
        for(int i = 0 ; i < inorder.length;i++){
            map.put(inorder[i],i);
        }
        return buildTree(preorder,0,preorder.length-1,inorder,0,inorder.length-1,map);
    }
    //i，j是先序的范围  x，y是中序的范围
    public TreeNode buildTree(int[] preorder,int i,int j,int[] inorder,int x,int y,HashMap<Integer,Integer> map){
        if(y < x){
            return null;
        }
        //先序的第一个节点是一棵树的根节点
        TreeNode p = new TreeNode(preorder[i]);
        //找到根节点在中序的位置mid
        int mid = map.get(preorder[i]);
        /**
        int mid = 0;
        for(mid = x; mid <= y;mid++){
            if(inorder[mid] == preorder[i]){
                break;
            }
        }*/
        //对于中序而言，[x,mid-1]是左子树元素 [mid+1,y]是右子树元素
        //对于先序而言，左子树中元素个数是mid-x,左子树第一个元素下标是i+1,总共mid-x个元素，下标范围是[i+1,i+mid-x]
        //右子树的范围是[i+mid-x+1,j]
        p.left = buildTree(preorder,i+1,i+mid-x,inorder,x,mid-1,map);
        p.right = buildTree(preorder,i+mid-x+1,j,inorder,mid+1,y,map);
        return p;
    }
}
解答成功:
            执行耗时:1 ms,击败了99.18% 的Java用户
            内存消耗:41 MB,击败了32.52% 的Java用户