
文章前后关联性较强,后文都是在前文的几何概念上展开。建议顺序阅读
文章目录
什么是矩阵乘法
矩阵乘法的几何意义
由上文可知,矩阵是一种线性变换,若矩阵乘变量则会对变量进行线性变换。而矩阵乘矩阵,其实就是对一个线性变换进行线性变换,即线性变换的复合 (我们同样可以通过追踪基向量的变换来表示这种复合变换)

(注意:矩阵乘法从右到左读,就像复合函数 f ( g(x) ) )
矩阵乘法运算上的几何意义
矩阵乘矩阵,是对一个线性变换进行线性变换,即对前一个线性变化的基分别进行线性变化
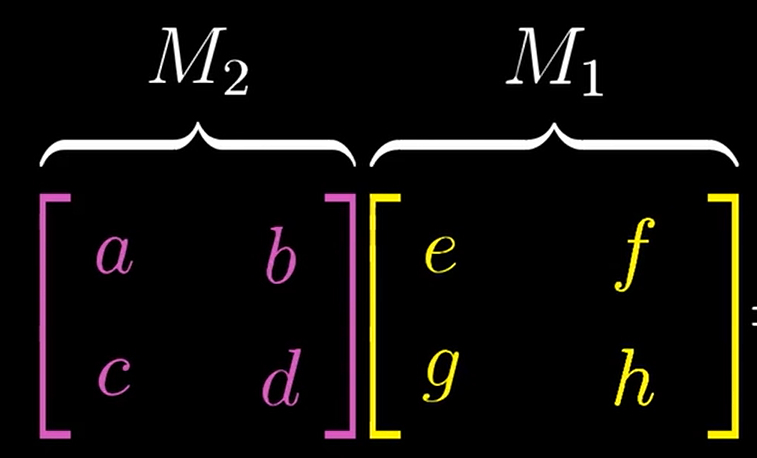
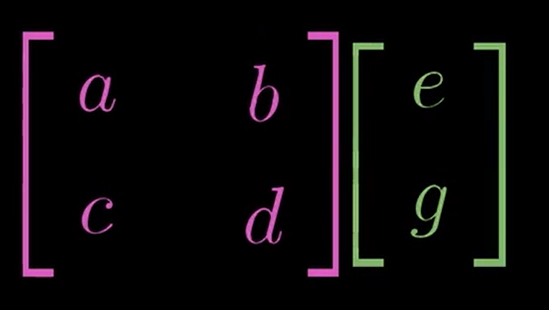
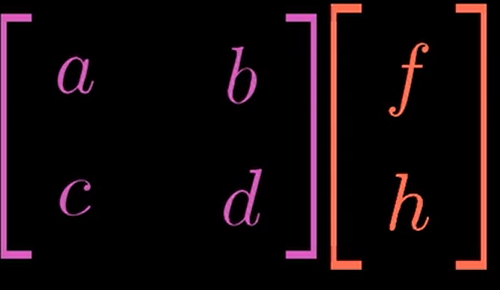
矩阵乘法的运算律的几何视角证明
无交换率 AB!=BA
易得矩阵乘法无交换律,因为易知线性变换的前后作用顺序不同造成的结果是不同的
有结合律 (AB) C = A (BC)
(AB) C —> C变换的基础上进行(AB)的复合变换,等价于C变换进行B变换再进行A变换(复合变换的几何意义)
A (BC) —> (BC)复合变换的基础上进行A变换,等价于C变换进行B变换再进行A变换(复合变换的几何意义)
因此二者都等价于 (ABC) ,即C变换先进行B变换再进行A变换
什么是行列式
行列式的几何意义
行列式表示的是一个线性变换对空间的挤压拉伸程度
二阶行列式:平行四边形的面积
三阶行列式:平行六面体的体积
矩阵的行列式的值 就是其代表的线性变换 对某一块空间(面积/体积)的 缩放比例
我们经常使用原基向量构成的1*1小方块作为基准来谈缩放比例,因为根据网格线平行且等距,1 *1小方块的缩放比例与其他所有特定的空间的缩放比例都相同
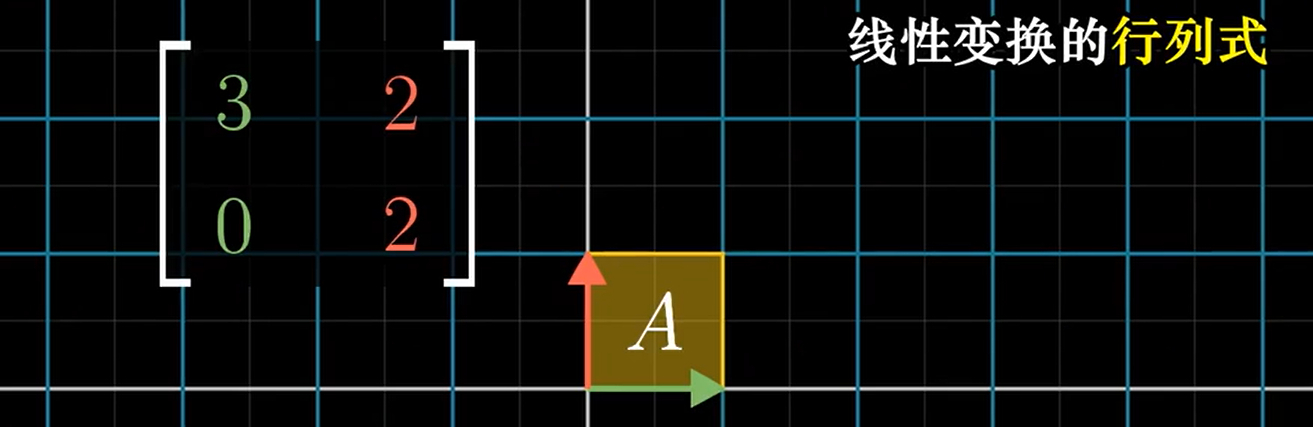
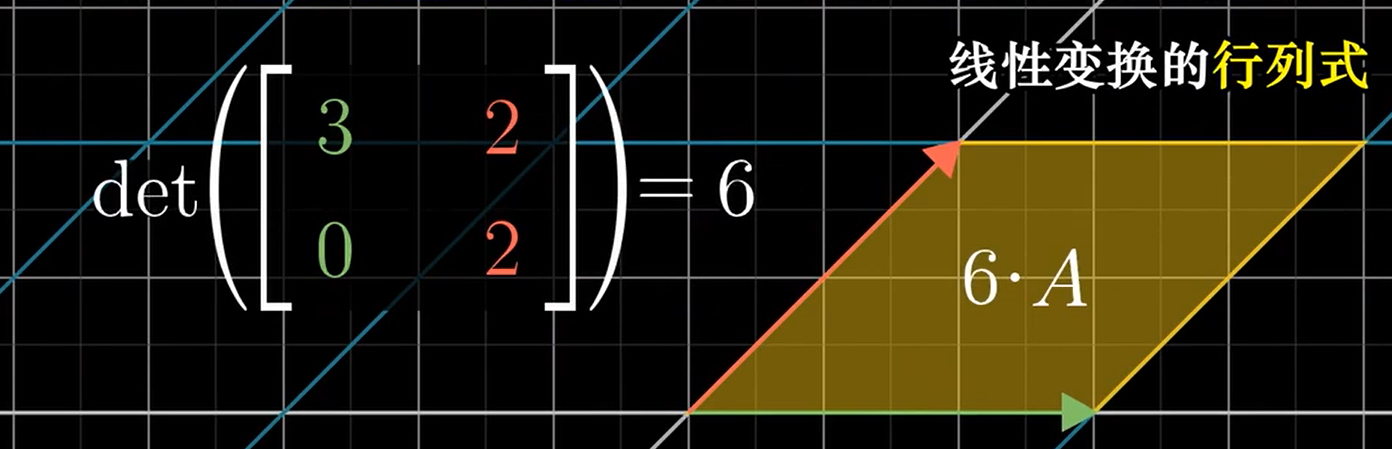 ## 行列式为0的特殊情况:
## 行列式为0的特殊情况:
(将空间的缩放比例为0,即降维)

行列式为负数的情况:
(基向量 i 和 j 的位置关系改变,空间的定向在线性变换中被改变,动态体现就是:空间在线性变换中转了个面)

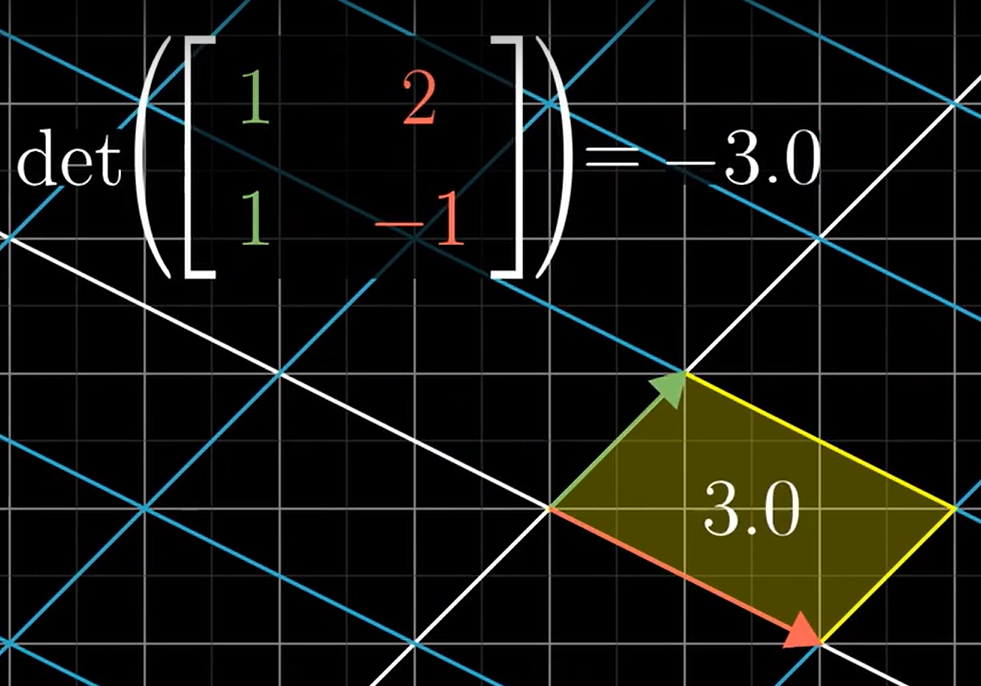
(二维中:一般基向量 i 在 j 的右边,如图变换后 i 在 j的左边,位置关系变换,空间的定向变换)
(三维中:空间的定向由右手法则判定)
什么是逆矩阵
线性方程组
线性代数之所以在很多个领域都会应用的主要原因是:它可以解特定的方程组(线性方程组)(注意:线性方程组中的方程只允许出现数乘和相加的操作,类似x2,sinx等式子是不能出现的)
线性方程组的求解可以写成矩阵与向量相乘等于一个向量的新形式
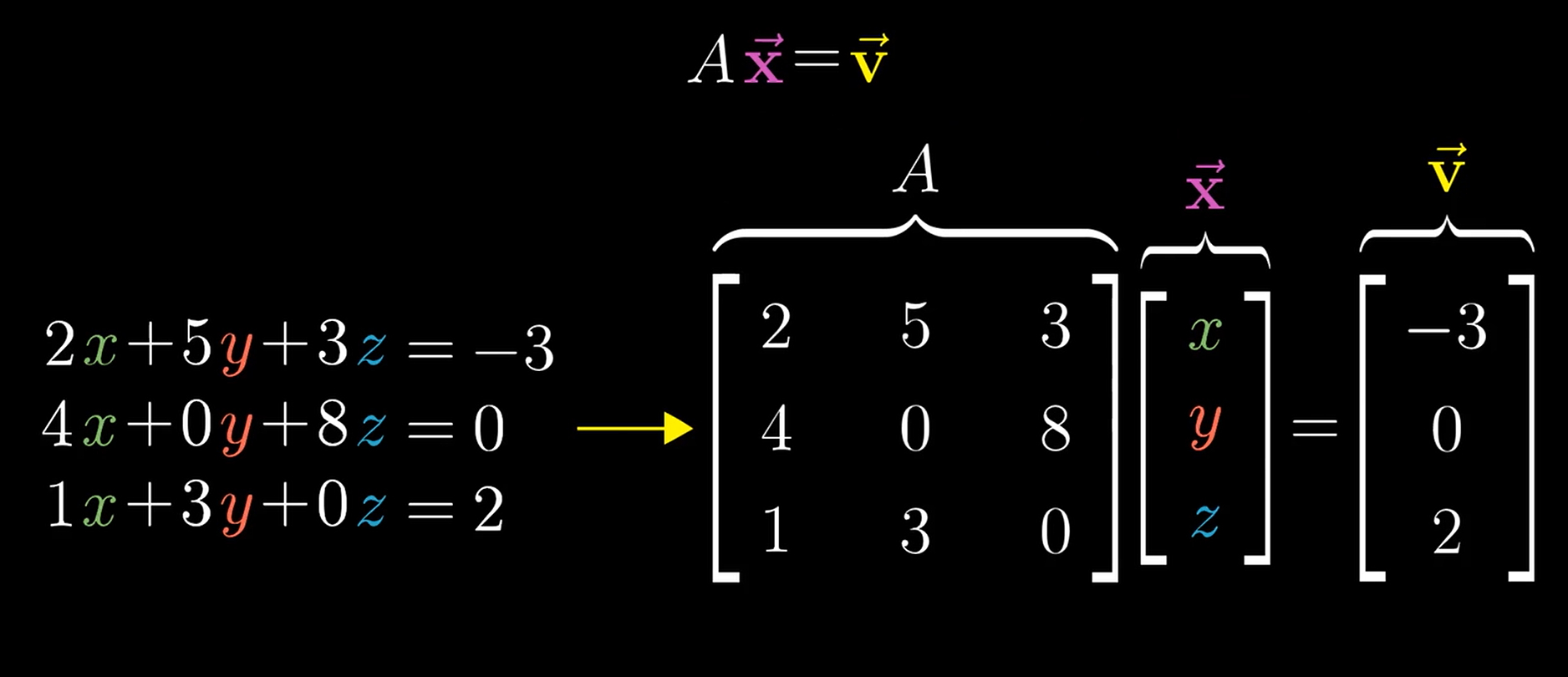
这样一来其线性方程组的几何意义就是:常数矩阵A将未知数向量 x经过线性变换后,与常数向量 v重叠
秩与列空间
秩(rank) — 描述线性变换后空间的维度大小。
eg: det(A) = 0, 当rank = 1时,A矩阵将空间压缩为一维直线,而当rank = 2时,A 矩阵将空间压缩为二维平面
列空间 — 矩阵的列空间是 矩阵所有可能的变换结果的集合(变为点,变为线,变为面等等)
(之所以称之为“ 列空间”的原因:矩阵所有可能变换出的空间,其实就是其列(基向量)张成的空间)
因此秩更准确的定义是:列空间的维度
秩与零空间
当秩达到最大值时,意味着秩与列数相等,称为满秩
原点处的情况:
-
满秩矩阵下:
由于线性变换中原点的位置不变,因此零向量在满秩矩阵的作用下仍位置不变,原点处只存在一个零向量 (满秩矩阵下唯一位置不变的向量) -
非满秩矩阵下:
一系列的向量在降维的变换中变为零向量。原点处可能压缩了一个直线的向量甚至可能压缩了一平面的向量!
经过矩阵变换后落在原点的向量构成矩阵的零空间或核

线性方程组的求解—逆矩阵
使用 Ax = v时有两种情况:
-
当det(A)!= 0 , 即线性变换未将空间降维,此时只存在一个对应的x,方程只有一个解
这时在空间中只存在一个x我们可以通过倒带的方式由v找到x。
这里说的倒带,其实指的是一种线性变换 — 逆矩阵 A-1 ,(A-1的核心是满足 A-1A = I)
此时x的解法为: A-1Ax = A-1 v —> x = A-1 v
-
当det(A)= 0 , 即线性变换将空间降维,此时没有逆变换,但当向量x,v恰好同在降维上后的空间中时,那么解仍然存在
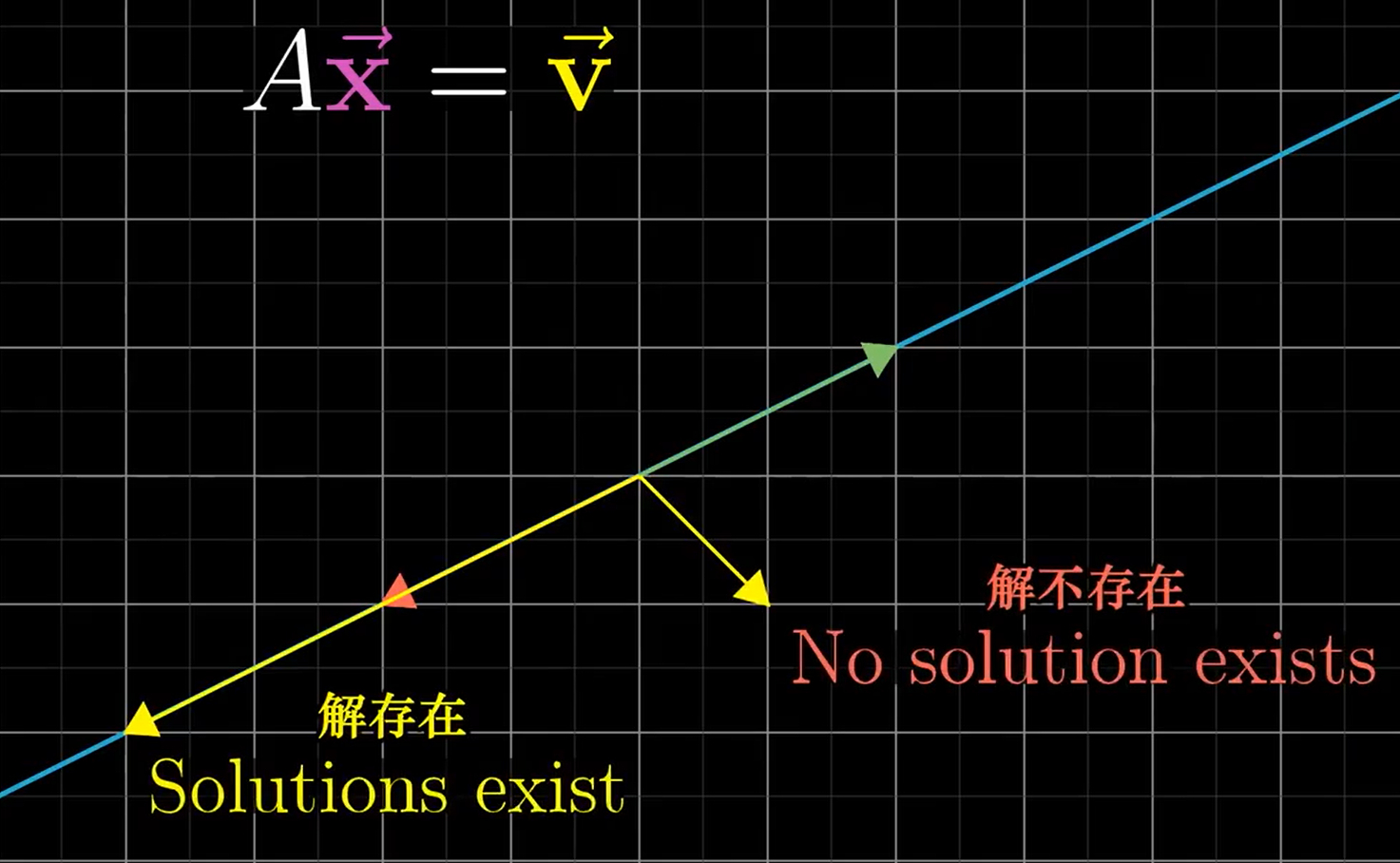
- 还有一种特殊的情况,当v 为零向量时,几何意义就是:x 变换后落在了零向量原点上,此时 x 就是矩阵的零空间
什么是点积
常见的点积几何意义解释:
点积是常用于解决向量指向和理解投影的有利几何工具
x • v 指 x在v上的投影 与 v 的乘积
(但是为什么点积会跟投影扯上关系呢 : )

将点积与线性变化相关联


如图:当且仅当原本图像上相互等距的一系列点,落到数轴上后也是等距的,多维到一维(一维数轴,上图为x轴)的变换是线性变换。
现在解决 矩阵值和向量值相同, 接着往下思考:
- 我们有x • v ,以v 所在的向量为我们降维变换后的数轴

- 为了求出该降维变换的矩阵,我们还是从基向量入手根据对称性原则,1*n矩阵的两元素 正是v 向量的坐标!
 <------->
<------->
- 故点乘x • v ,就是以 v向量坐标为矩阵元素的矩阵 对x 向量进行了线性变换(使x v共线) ,在图像上表现为,x线性变换至v所在直线上,即投影,在数值上表现为a * c + b *d,即向量对应相乘

启示:对偶性
向量的点乘中,向量对偶于一个高维到一维的线性变换
( 对偶性 :即一种出乎意料但又自然的对应关系)










