模型介绍

输入空间：$\mathcal{X}\subseteq \boldsymbol R^n$ 输入：$x=(x^{(1)},x^{(2)},\cdots,x^{(n)})^T\in\mathcal{X}$ 输出空间：$\mathcal{Y}={+1,-1}$ 输出：$y\in\mathcal{Y}$ 感知机：$$f(x)=\text{sign}(w\cdot x+b)=\begin{cases}+1,\quad w\cdot x+b\geq0\-1,\quad w\cdot x+b<0\end{cases}$$其中$w=(w^{(1)},w^{(2)},\cdots,w^{(n)})^T\in\boldsymbol R^n$称为权值（Weight），$b\in\boldsymbol R$称为偏置（Bias），$w\cdot s$表示内积$$w\cdot x=w^{(1)}x^{(1)}+w^{(2)}x^{(2)}+\cdots+w^{(n)}x^{(n)}$$ 假设空间：$\mathcal{F}={f|f(x)=w\cdot x+b}$ 参数空间：所有$w,b$组成的空间，是一个$n+1$维的空间

几何含义

线性方程：$$w\cdot x+b=0$$

• 特征空间$\boldsymbol R^n$中的一个超平面$\boldsymbol S$ 超平面是比它所处的环境空间小一维的子空间
• 法向量：$w$；截距：$b$

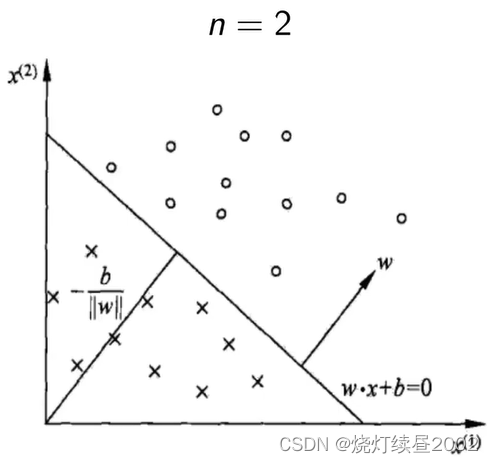
对于$n=2$有$x=(x^{(1)},x^{(2)})$，$w=(w^{(1)},w^{(2)})$ $\begin{aligned}w\cdot x+b=0&\Rightarrow(w^{(1)},w^{(2)})\cdot(x^{(1)},x^{(2)})+b=0\&\Rightarrow w^{(1)}x^{(1)}+w^{(2)}x^{(2)}+b=0\&\Rightarrow x^{(2)}=-\frac{w^{(1)}x^{(1)}}{w^{(2)}}-\frac b{w^{(2)}}\end{aligned}$ 图中$-\frac b{||w||}$中$||w||$表示$w$的欧式范数，即$||w||=\sqrt{{w^{(1)}}^2+{w^{(2)}}^2}$

流程图

学习策略

学习策略就是最小化损失函数，求得参数

$\forall x_0\int\boldsymbol R^n$到$\boldsymbol S$的距离（补充：点到超平面距离公式的推导）：$$\frac1{||w||}|w\cdot x_0+b|$$ 若$x_0$是正确的分类点，则$$\frac1{||w||}|w\cdot x_0+b|=\begin{cases}\frac{w\cdot x_0+b}{||w||},\quad y_0=+1\-\frac{w\cdot x_0+b}{||w||},\quad y_0=-1\end{cases}$$ 若$x_0$是错误分类点，则$$\frac1{||w||}|w\cdot x_0+b|=\begin{cases}-\frac{w\cdot x_0+b}{||w||},\quad y_0=+1\\frac{w\cdot x_0+b}{||w||},\quad y_0=-1\end{cases}=\frac{-y_0(w\cdot x_0+b)}{||w||}$$ 误分类点$x_i$到$\boldsymbol S$的距离$$-\frac1{||w||}y_i(w\cdot x_i+b)$$ 所有误分类点到$\boldsymbol S$的距离$$-\frac1{||w||}\sum_{x_i\in M}y_i(w\cdot x_i+b)$$ 其中，$M$表示所有误分类点的集合。$\frac1{||w||}$虽然不是固定的值，但不影响最后的结果，后面会提到。 损失函数：$$L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b)$$

条件

数据集的线性可分性 给定数据集$$T={(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)}$$若存在某个超平面$\boldsymbol S$$$w\cdot x+b=0$$能够将数据集的正负实例点完全正确的划分到超平面的两侧，即$$\begin{cases}y_i=+1,\quad\text{则}w\cdot x_i+b>0\y_i=-1,\quad\text{则}w\cdot x_i+b<0\end{cases}$$那么，称$T$为线性可分数据集；否则，称$T$为线性不可分