目录
哈喽
dfs乃何物?
DFS(Depth First Search) ,即 深度优先搜索 ,是一种遍历图的方式。
比如这张图(用鼠标写数字有点丑)
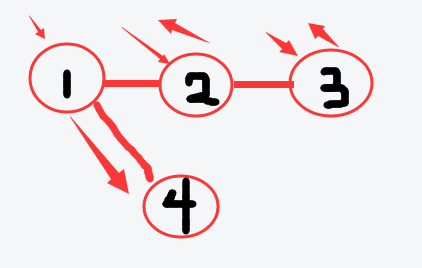
我们要找到4这个值
假设从1开始找
1没找到
再找2,2也没找到,
找3,3又没找到
发现已经走到头了
再一步一步回溯到1,走另外一条路,找到了4
总结一下,dfs会在搜索到新点时优先访问以改点为起点的子节点,并在所有子节点访问完成后回溯,可以看出,dfs和递归殊途同归。
相反地,有BFS(Breath First Search)广度优先搜索,用bfs访问上例时访问顺序为:1,2,4,3。程序会访问完当前节点的所有子节点,一层一层向下搜。
练练英语:
DFS will preferentially visit the child nodes starting from the change point when searching for a new point, and backtrack after all the child nodes are accessed. It can be seen that DFS and recursion come to the same destination.
In contrast, Breath First Search (BFS) is the breadth-first Search. When BFS is used to access the above example, the access sequence is 1,2,4,3. The program accesses all the children of the current node, level by level down.
懂了吗?就这么简单
DFS算法过程:
1、任选一顶点作始点 v ,访问该顶点
2、沿深度方向,依次遍历 v 的未访问邻接点——直到本次遍历结束
3、一次遍历完时,若有未访问顶点:任选一个未访问顶点作起始点,GOTO第二步
dfs基本框架
基本写法代码是这样的
void dfs(int u){//u:当前节点
vis[u]=true;
for(int& v:g[u]){//访问u连到的每个节点
if(!vis[v]) dfs(v);
}
}
其实它的代码很少,主要是理解
就这么简单,看题
题目1

思路其实比较简单,有点类似于穷举法。我们构建一棵数,每一层依次增加一个没有枚举的数,当到达底层的时候就是一个答案。
比如我们先将第一个数填1,然后由于还有数未填入,继续深入到达下一层。下一层由于第一个数1已经枚举,我们枚举第二个数2。然后继续进入第三层,枚举第三个数3,由于已经把所有的数都枚举完,我们此时要进行一个回溯,回到第二层。由于第二层中只有一个数没有枚举,因此我们已经枚举完第二层的所有可能,因此回溯到第一层。接下来将第二位置填入未被枚举的3,以此反复。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
//用一个path数组来存储每次到底层的路径
int path[N];
//用一个布尔数组来存储每次已经遍历的点,默认是false
bool st[N];
int n;
//u表示当前的层数
void dfs(int u)
{
//当已经到达最底层了,溯回并输出路径
if( u == n )
{
for(int i = 0 ; i < n ; i++) printf("%d " , path[i] );
//作用跟printf("%s\n",s),默认帮你换行
puts("");
//溯回上一层
return;
}
else
{
//这里从第一个数开始循环
for(int i = 1; i <= n ; i++)
{
//如果该数字未被访问,就使用
if( !st[i] )
{
path[u] = i;
//标记第i个数已经被使用
st[i] = true;
//进入下一层
dfs( u + 1 );
//还原现场
st[i] = false;
}
}
}
}
int main()
{
cin >> n;
dfs(0);
return 0;
}题目2 n-皇后问题
题目
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
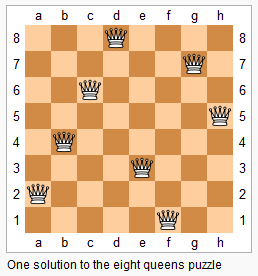
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..代码
分析见代码注释
#include<iostream>
using namespace std;
const int N = 20;//对角线的个数是2n - 1
char g[N][N];//存储当前的图
bool col[N], dg[N], udg[N];//列和对角线以及反对角线是否有皇后(true 有,false无)
int n;
void dfs(int u)
{
if(u == n)//表示已经搜了n行,故输出这条路径
{
for(int i = 0; i < n; i ++)puts(g[i]);
puts("");
return;
}
for(int i = 0; i < n; i ++)
{
if(!col[i] && !dg[u + i] && !udg[n - u + i])//对角线为 n- u + i, 反对角线下标为 u + i
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
//还原现场
col[i] = dg[u + i] = udg[n - u + i] = false;
g[u][i] = '.';
}
}
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)
for(int j = 0; j < n; j ++)
g[i][j] = '.';
dfs(0);
return 0;
}
//dfs与递归类似 寻路
好了,思路也讲完了,题目也做完了
按照常理,嘿嘿,到了快乐的coding时间了
相信各位都听说或用过寻路吧
主要就是通过栈来存储路径,辅助地图更改方向与记忆路是否走过
效果(我用的编译器是VS2019),运行程序会有一个#,是会动的,沿着我画出的路径移动,最终找到出口


代码
#include <iostream>
#include <stack>
#include <Windows.h>
using namespace std;
#define ROWS 12//x
#define COLS 12//y
struct MyPoint {
int x;
int y;
//MyPoint(int xx, int yy) :x(xx), y(yy) {};
};
//辅助地图
enum dirent { p_up, p_left, p_down, p_right };
struct pathNode {
int val;//
dirent dir; //方向
bool isFind;//是否走过
};
//打印地图
void printMap(int map[][12], MyPoint pos)
{
system("cls");
for (int i = 0; i < ROWS; i++)
{
for (int j = 0; j < COLS; j++)
{
if (i == pos.x && j == pos.y)
{
cout << "#";
}
else if (map[i][j])
{
cout << "*";
}
else
{
cout << " ";
}
}
cout << endl;
}
Sleep(200);
}
int main()
{
/*
地图: 数组
1墙 0路
*/
int map[ROWS][COLS] = {
{1,1,1,1,1,1,1,1,1,1,1,1},
{1,0,1,1,1,1,1,1,1,1,1,1},
{1,0,1,1,0,1,1,1,1,1,1,1},
{1,0,1,1,0,1,1,1,1,1,1,1},
{1,0,1,1,0,1,1,0,0,0,0,1},
{1,0,1,1,0,1,1,1,1,1,0,1},
{1,0,0,0,0,0,0,0,1,1,0,1},
{1,0,1,1,0,1,1,0,1,1,0,1},
{1,0,1,1,0,1,1,0,1,1,0,1},
{1,0,1,1,0,1,0,0,0,0,0,1},
{1,0,1,1,0,1,0,1,1,1,0,1},
{1,1,1,1,1,1,1,1,1,1,1,1}
};
MyPoint begPos = { 1,1 };
MyPoint endPos = { 10,10 };
//printMap(map,begPos);
pathNode pathMap[ROWS][COLS] = { 0 };
for (int i = 0; i < ROWS; i++)
for (int j = 0; j < COLS; j++)
{
pathMap[i][j].val = map[i][j];
}
MyPoint currentPos = begPos;
MyPoint searchPos; //试探点
stack<MyPoint> stack;
stack.push(begPos);
pathMap[begPos.x][begPos.y].isFind = true;//标记走过
bool isFindEnd = false;
while (!isFindEnd)
{
printMap(map, currentPos);
//确定试探点
searchPos = currentPos;
switch (pathMap[currentPos.x][currentPos.y].dir)
{
case p_up:
searchPos.x--;
pathMap[currentPos.x][currentPos.y].dir = p_left;
break;
case p_left:
searchPos.y--;
pathMap[currentPos.x][currentPos.y].dir = p_down;
break;
case p_down:
searchPos.x++;
pathMap[currentPos.x][currentPos.y].dir = p_right;
break;
case p_right:
searchPos.y++;
if (pathMap[searchPos.x][searchPos.y].val != 0 || //不是路
pathMap[searchPos.x][searchPos.y].isFind == true) //以前路过
{
stack.pop();
currentPos = stack.top();
}
break;
}
//判断试探点
if (pathMap[searchPos.x][searchPos.y].val == 0 && //路
pathMap[searchPos.x][searchPos.y].isFind == 0) //未走过
{
currentPos = searchPos;
//走
//标记走过
pathMap[currentPos.x][currentPos.y].isFind = true;
//入栈
stack.push(currentPos);
}
//判断是否终点
if (currentPos.x == endPos.x &&
currentPos.y == endPos.y)
isFindEnd = true;
//判断是否栈为空
if (stack.empty())
{
cout << "未找到路径" << endl;
break;
}
}
//显示路径
if (isFindEnd)
{
cout << "path:";
while (!stack.empty())
{
cout << stack.top().x << "," << stack.top().y << endl;
stack.pop();
}
}
return 0;
}










