前言
本栏目将记录博主暑假从0开始刷力扣的算法题,每一条题目我都会把知识点抽丝剥茧地进行分析,以便大家更好的理解和学习,话不多说,肝!
1.杨辉三角I
题目:
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
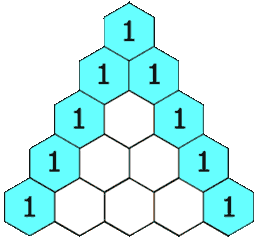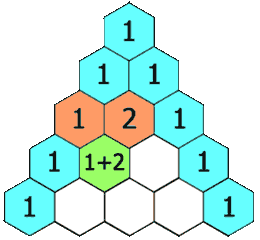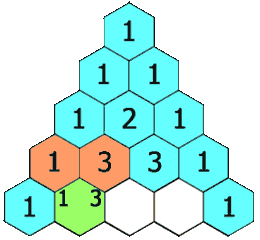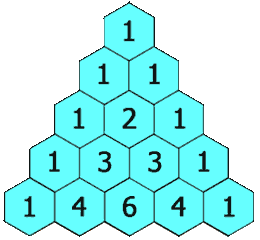
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
解题思路:
杨辉三角的性质: 每个位置上的数等于它上方两个数之和。
代码(go)
func generate(numRows int) [][]int {
ans := make([][]int, numRows)
for i := range ans {
ans[i] = make([]int, i+1)
ans[i][0] = 1
ans[i][i] = 1
for j := 1; j < i; j++ {
ans[i][j] = ans[i-1][j] + ans[i-1][j-1]
}
}
return ans
}
下面是代码的具体解析
j 从 1 开始,因为杨辉三角每一行的首尾元素都是 1,不需要重新计算。
2.杨辉三角II
题目:
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

方式一:递推
解题思路:
杨辉三角的性质: 每个位置上的数等于它上方两个数之和。
此题和上面那道杨辉三角解法类似,区别就是此题rowIndex是索引,所以需要+1
代码(go):
func getRow(rowIndex int) []int {
C := make([][]int, rowIndex+1)
for i := range C {
C[i] = make([]int, i+1)
C[i][0], C[i][i] = 1, 1
for j := 1; j < i; j++ {
C[i][j] = C[i-1][j-1] + C[i-1][j]
}
}
return C[rowIndex]
}
方式二:
利用滚动数组进行优化
解题思路:
注意到对第 i+1 行的计算仅用到了第 i 行的数据,因此可以使用滚动数组的思想优化空间复杂度。
优化后的代码只需要计算两行的杨辉三角即可,可以节省内存空间
代码(go)
func getRow(rowIndex int) []int {
var pre, cur []int
for i := 0; i <= rowIndex; i++ {
cur = make([]int, i+1)
cur[0], cur[i] = 1, 1
for j := 1; j < i; j++ {
cur[j] = pre[j-1] + pre[j]
}
pre = cur
}
return pre
}
代码解析:
pre:前一行的数组。cur:当前行的数组,随着每一行的生成而更新。cur[j] = pre[j-1] + pre[j]:根据杨辉三角的性质,当前行的第j列的值等于上一行的第j-1列和第j列的和。pre = cur:将当前行cur赋给pre,作为下一行的基础。
方式三:
只用一个数组,进一步优化
解题思路:
我们使用一维数组,然后从右向左遍历每个位置。
每个位置的元素res[j] += 其左边的元素 res[j−1]。 row[j] += row[j-1]
为啥不从左向右遍历呢?因为如果从左向右遍历,那么左边的元素已经更新为第 i 行的元素了,而右边的元素需要的是第 i−1 行的元素。故从左向右遍历会破坏元素的状态。

代码(go)
func getRow(rowIndex int) []int {
row := make([]int, rowIndex+1)
row[0] = 1
for i := 1; i <= rowIndex; i++ {
for j := i; j > 0; j-- {
row[j] += row[j-1]
}
}
return row
}
3.移动零
题目:
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 :
输入: nums =[0,1,0,3,12]输出:[1,3,12,0,0]
解题思路:
这个思路类似于快速排序,可以去小破站看一下视频
快速排序

(图片出自王尼玛)
代码(java)
class Solution {
public void moveZeroes(int[] nums) {
if(nums==null) {
return;
}
//第一次遍历的时候,j指针记录非0的个数,只要是非0的统统都赋给nums[j]
int j = 0;
for(int i=0;i<nums.length;++i) {
if(nums[i]!=0) {
nums[j++] = nums[i];
}
}
//非0元素统计完了,剩下的都是0了
//所以第二次遍历把末尾的元素都赋为0即可
for(int i=j;i<nums.length;++i) {
nums[i] = 0;
}
}
}
这道题花费了我两小时的时间,因为我先了解了快速排序的原理,然后再学习了双指针的思想,最后卡到的最简单自增自减运算符上...
注意:
for循环的设计就是先执行循环体内的代码,然后再递增计数器
所以其实在 for(int i=0;i<nums.length;++i) 这段语句中 无论是++i,还是i++都是可以运行的。
然后在 nums[j++] = nums[i]这段语句中,其实j是先执行,然后再修改值的。以第二次循环为例,当i = 1的时候,遇到非0的元素,所有i 和 j 要交换元素 所以就是 num[0] = num[1] 然后j++ 变成1
4.区域和检索 -数组不可变
题目:
示例 :
输入: ["NumArray", "sumRange", "sumRange", "sumRange"] [[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]] 输出: [null, 1, -1, -3]
解题思路:
这里用到前缀和思想,可以理解为高中学的数列

我们可以画一个sum[0]到sum[6]的数列,以【2,5】为例(此处的2,5是索引值)
所以就是sum[6]-sum[2]
示例中的数组有6个元素,假如要计算索引2到5之间的总和(包含2到5),我们可以先计算索引为数组开始到5的总和减去数组开始到索引为2(不能包含索引2)
代码(java)
class NumArray {
int[] sums;
public NumArray(int[] nums) {
int n = nums.length;
sums = new int[n + 1];
for (int i = 0; i < n; i++) {
sums[i + 1] = sums[i] + nums[i];
}
}
public int sumRange(int i, int j) {
return sums[j + 1] - sums[i];
}
}
5.第三大的数
题目:
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。
示例 1:
输入:[3, 2, 1] 输出:1 解释:第三大的数是 1 。
示例 2:
输入:[1, 2] 输出:2 解释:第三大的数不存在, 所以返回最大的数 2 。
示例 3:
输入:[2, 2, 3, 1] 输出:1 解释:注意,要求返回第三大的数,是指在所有不同数字中排第三大的数。 此例中存在两个值为 2 的数,它们都排第二。在所有不同数字中排第三大的数为 1 。
方式一:
Set 去重 + 排序
解题思路:
先使用 Set 对重复元素进行去重,然后对去重后的元素进行排序,并返回第三大的元素。
代码(Java)
class Solution {
public int thirdMax(int[] nums) {
Set<Integer> set = new HashSet<>();
for (int x : nums) set.add(x);
List<Integer> list = new ArrayList<>(set);
Collections.sort(list);
return list.size() < 3 ? list.get(list.size() - 1) : list.get(list.size() - 3);
}
}
HashSet 基于 HashMap 来实现的,是一个不允许有重复元素的集合。
// 创建 HashMap 对象 Sites
HashMap<Integer, String> Sites = new HashMap<Integer, String>();ArrayList 类是一个可以动态修改的数组,与普通数组的区别就是它是没有固定大小的限制,我们可以添加或删除元素。
使用一个增强型for循环遍历数组nums,将每个元素添加到set中。
for (int x : nums) set.add(x);假如数组为【1,2,3】,那么执行
return list.size() < 3 ? list.get(list.size() - 1) : list.get(list.size() - 3); 这里的 list.size() - 3 实际上是 3 - 3 = 0,而 list.get(0) 会返回列表中的第一个元素,即 1。
方式二:
有限变量 + 遍历
解题思路:(大家可以参考一下宫水三叶的解析)
代码(Java)
class Solution {
long INF = (long)-1e18;
public int thirdMax(int[] nums) {
long a = INF, b = INF, c = INF;
for (int x : nums) {
if (x > a) {
c = b; b = a; a = x;
} else if (x < a && x > b) {
c = b; b = x;
} else if (x < b && x > c) {
c = x;
}
}
return c != INF ? (int)c : (int)a;
}
}










