CS229 Lecture Note
Ora Yang
译者注:翻译斯坦福CS229对应讲义,如有错误,欢迎留言指正~(持续更新中)
现在让我们来谈谈分类问题。它就像回归问题一样,只是我们要预测的y值只是一小部分的离散值。现在我们将把重点放在二分类问题上,在这个问题上y只取两个值0和1。(我们在这里说的大部分内容也适用与多类情况)。例如,我们努力为邮件建立一个垃圾分类器,那么可能是电子邮件的一些特征,如果是垃圾邮件y可能是1,否则是0。0也被称为负类并且1为正类。它们有时候也用符号"-"和"+"表示。给定,相应的也被成为一个训练样本的标签。
- 逻辑回归
我们可以处理分类问题,忽略y是离散值的事实,并且使用我们原先的线性回归算法来尝试在给定x的情况下预测y值。但是这很容易构造出这种方法不能很好执行的样本。直观地说,当我们知道y ∈ {0, 1}时,,取值大于0或者小于1都毫无意义。
为了解决这个问题,我们改变假设的形式,我们将选择
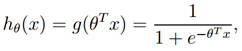
其中,
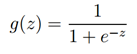
被称为逻辑函数或双弯曲函数,如下显示g(z)的图形:
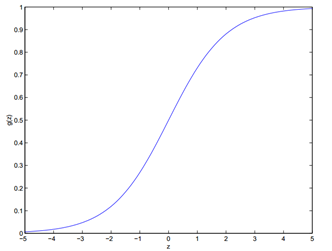
注意当z → ∞时,g(z)趋向于1,并且当z → −∞时,g(z)趋向于0。而且g(z)也就是h(z)也总是取值在0和1之间。和之前一样,我们保留了=1的约束,所以有
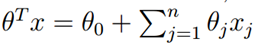
现在,让我们选择g为给定项,其他从0到1平稳递增地函数也可以被使用,但是由于接下来我们将会看到的一些原因(当我们讨论GLMS时以及当我们讨论生成学习算法时),逻辑函数的选择是相当自然的。再继续之前,这儿给出了sigmoid函数的导数的一个有用的性质,我们把它写成g′:
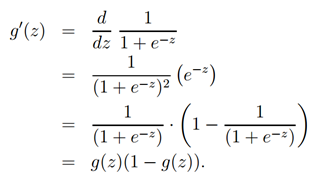
那么考虑到逻辑回归模型,我们如何来拟合呢?根据一组假设,我们可以得出最小二乘回归是最大似然估计数,我们通过一组概率假设来赋予我们的分类模型,然后通过最大似然来拟合参数。
我们假设:
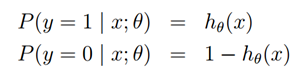
请注意,这可以更简洁地写成
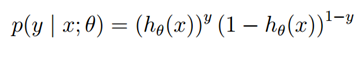
假设m个样本是独立生成的,那么我们可以写下参数的最大似然估计为
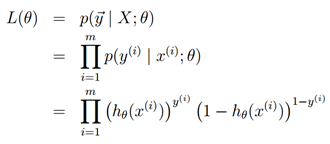
和以前一样,这样就更容易最大化log似然
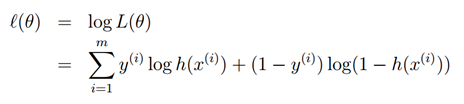
我们如何最大化似然值,与线性回归中的推导类似,我们可以使用梯度上升法。以矢量表示法书写,因此我们的更新将由
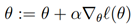
给出。(注意公式中正号而不是负号,因此我们是在最大化一个函数而不是最小化)。让我们以一个训练样本作为开头,并且利用导数来推导随机梯度上升。
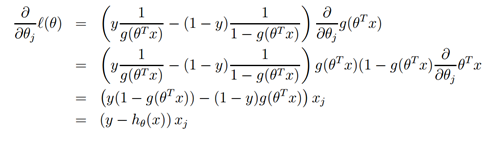
上面我们使用了
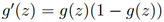
,这就给我们一个随机梯度上升规则。
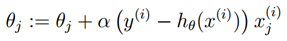
如果我们将这与LMS更新规则比较,会发现它们是一样。但是这个不同的算法,因为现在被定义成的非线性函数。尽管如此,对于一个完全不同的算法和学习问题,我们最终得到相同的更新规则,这有点让人吃惊。这是巧合还是说背后有着更深层次的原因。当我们得到GLM模型,我们就会回答这个问题。
- 题外话:感知机学习算法
我们现在简单地讨论一个历史上有趣的算法,当我们讨论学习理论的时候,之后还会回来。考虑逻辑回归算法使其强制输出0或1。为了达到这个目的,将g(z)改变成阈值函数看上去比较自然:
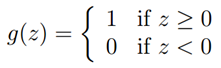
如果我们像以前那样让
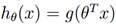
,但是使用这个修改后的g的定义,如果我们使用更新规则
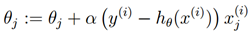
然后我们就有了感知机学习算法。
在上个世纪60年代,这个感知机被认为是一个粗略的模型用来解释大脑中的单个神经元是如何工作的。考虑到算法的简单性,当我们我们在课堂上讲学习理论时,它也会为我们的分析提供一个起点。注意,尽管感知机学习算法与我们讨论的其他算法相似,但它实际上是与逻辑回归和最小二乘线性回归完全不同的算法。特别地,很难赋予感知器的预测以有意义的概率解释,或者将感知器作为最大似然估计算法。
- 另一种最大化ℓ(θ)的算法
回到用g(z)作为sigmoid函数的逻辑回归算法,让我们来讨论一个不同的最大化ℓ(θ)的算法。
为了让我们开始,我们采用牛顿法来寻找一个函数的零点。具体来说,假设我们有一个函数f : R → R,并且我们希望来寻找一个值,来使得=0,此处,θ ∈ R,为实数。牛顿法执行以下更新:
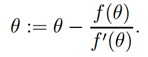
这个方法有一个自然的解释,它通过一个在当前的猜想θ处与函数f相切的线性函数,求解线性函数等于0的点,并让下一个θ作为上一个线性函数等于0的点来近似求解。
这儿时牛顿法的一系列图:
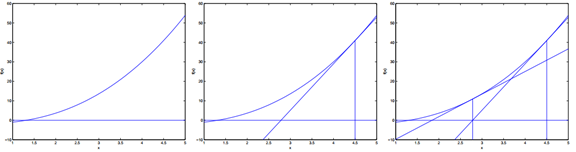
在最左边的图,我们可以看到函数f沿着y=0的画图。我们尝试去找到f(θ)=0的点。这个θ值是1.3。假设我们用θ=4.5来初始化,牛顿法在θ=4.5处拟合了一条与f相切的直线,然后求出这条直线值为0的地方(中间那幅图)。这个给了下一个θ的猜测,大概为2.8。
最右边那幅图给出有一次迭代的结果,θ更新到1.8。经过几次迭代后,我们快速地接近θ=1.3。
牛顿法给出了求f()=0的方法,如果我们想用它来最大化某个函数ℓ呢?它的极大值对应于第一个导数为0的点。因此通过让

,我们可以使用相同的算法来最大化ℓ,并且我们获得了更新规则:
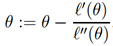
最后,在我们的逻辑回归设定中,是矢量值,因此我们需要将牛顿法推广到这个设定上。牛顿法对多维环境的推广(也被称为牛顿-拉普森法)概括为:
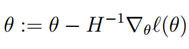
此处,
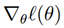
和往常一样,是ℓ(θ)对的偏导。并且H是一个n x n的海塞矩阵(假如我们包含截距项就是 n+1 x n+1的矩阵):
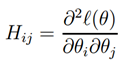
牛顿法通常比批量梯度下降能更快地收敛,并且可以只迭代更少的次数便能达到最小值。一次牛顿法的迭代可能比一次梯度下降代价更高,因为牛顿法需要找到并转换一个n x n的海塞矩阵,但是只要n不是太大,总体来说它快地多。当牛顿法被应用到最大化逻辑回归中的log似然函数ℓ(θ)时,这个最终的方法也被称为费舍尔计分法。










