数据结构小记【Python/C++版】——图结构篇

一，基础概念

1.图的简介

图没有起始位置和终止位置，是由顶点和边组成的一种非线性数据结构。

2.图结构的常见概念

(先大概了解一下，后面可以结合图示对照看看)： 

顶点(Vertex/Node)：顶点又称节点，是图的基础部分。

边(Edge)：两个顶点之间的连线。

权重(Weight)：边上可以附带的权重大小，用来表示从一个顶点到另一个顶点的成本。

相邻(Adjacency)：同一条边两端的顶点被称为相邻或者邻接。

路径(Path)：由边连接的顶点组成的序列。

度(Degree)：连接到一个顶点的边的数量。

入度(Indegree)：按传入方向连接到顶点的有向边的总数。

出度(Outdegree)：按传出方向连接到顶点的有向边的总数。

3.图的等式表示

图结构可以用等式表示：G=(V, E)。

G是图结构的抽象表示。

V是图中的顶点集合，一般用数组存储，所以V常见于顶点数组。

E是相邻顶点的集合，E中的元素也表示他们连接而成的边。例如E中的一个元素是(u, v)，表示顶点u和顶点v连接成的边。如果是有方向的边，(u, v)和(v, u)表示的是不同方向的两条边，如果是无方向的边，则(u, v)和(v, u)表示的是同一条边。例如下图中的(1, 2)和(2, 1)表示的是相同的边。

该图有一组顶点V={1,2,3,4,5}和一组边E={(1,2),(1,3),(2,3),(2,4),(2,5),(3,5),(4,5)}。

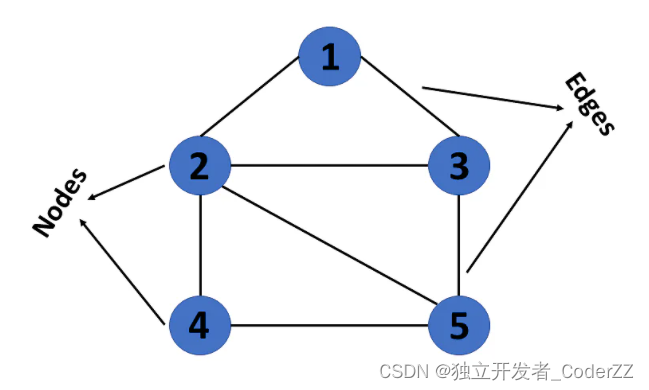
二，常见的图结构分类

a.无向图

任意两个顶点之间的边不带方向。

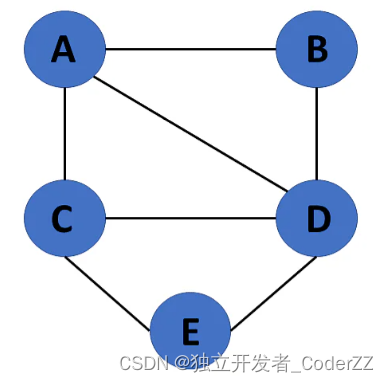
b.有向图

任意两个顶点之间的边区分方向。

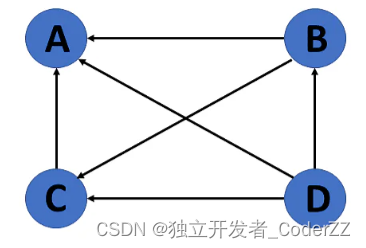
c.连通图

图数据结构的一个顶点与任何其他顶点之间存在可以到达的路径、

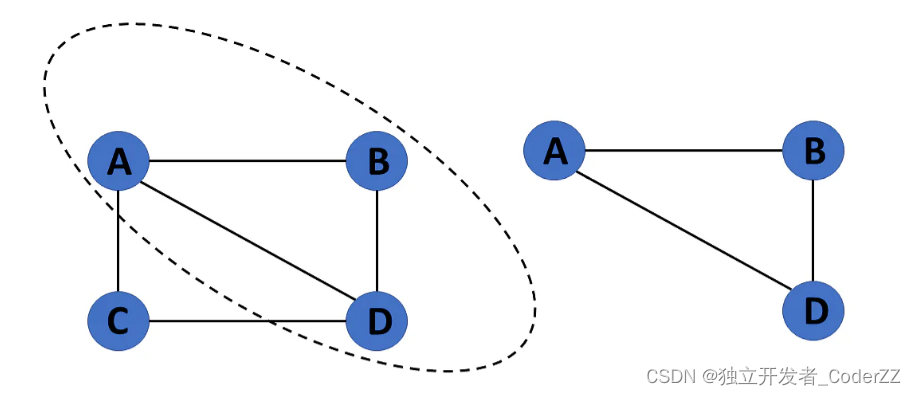
d.子图

顶点和边的组合是另一个图的子集

e.加权图

每条边都有一个权重，表示遍历该边的成本

三，图的常见表示方式

基于二维数组的表示方式——邻接矩阵(Adjacency Matrix)

基于链表的表示方式——邻接表(Adjacency List)

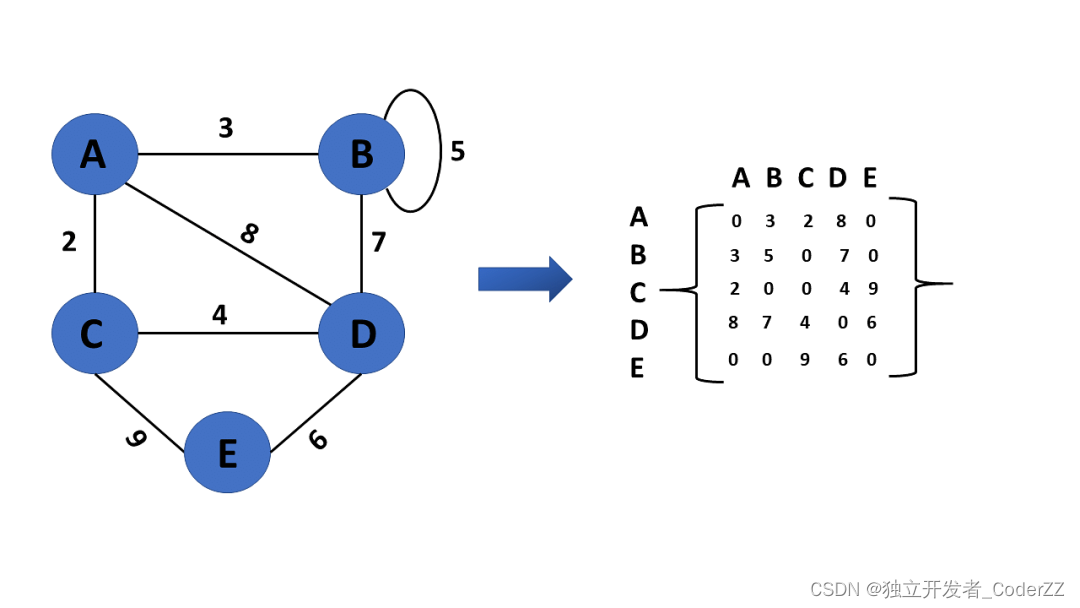
1.邻接矩阵

邻接矩阵用于显示哪些节点彼此相邻。

矩阵的行和列都是图的顶点列表，矩阵中不为0的地方表示顶点之间互相连接，即矩阵中不为0的地方表示边。

a.无向图的邻接矩阵

如果顶点a和顶点b之间存在边：AdjMatrix(A, B)=AdjMatrix(B, A)=1

b.有向图的邻接矩阵

如果存在顶点b到顶点a的边：AdjMatrix(B, A)=1

如果不存在顶点a到顶点b的边：AdjMatrix(A, B)=0

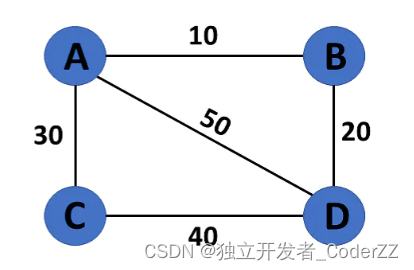
c.加权无向图的邻接矩阵

如果顶点a和顶点b之间存在边，且边的权重为3：AdjMatrix(A, B)=AdjMatrix(B, A)=3

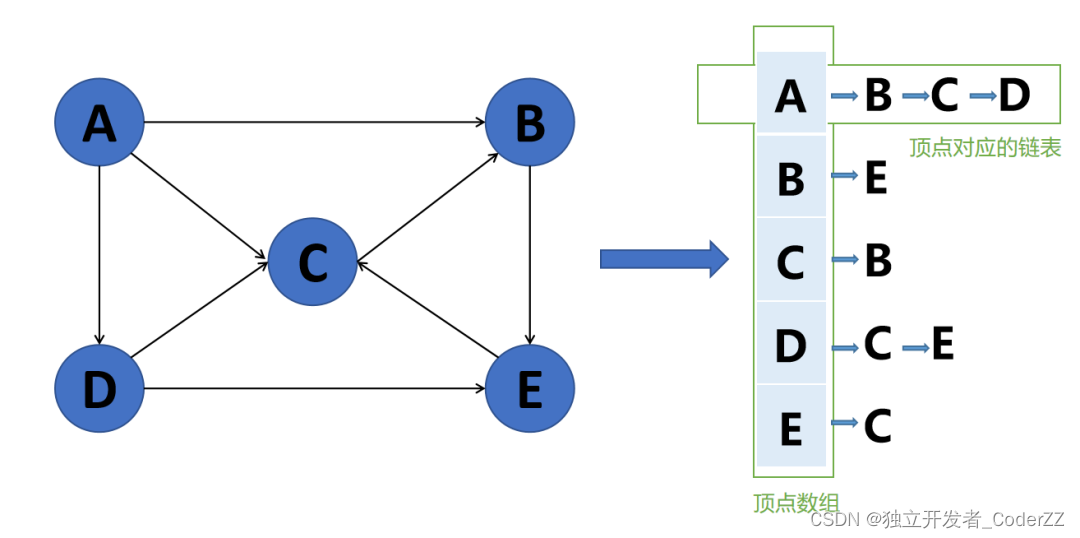
2.邻接表

通俗说就是每个顶点专门有一个列表来记录自己有哪些邻居，这个列表常用链表结构来实现。此结构维护了两张表：

1.包含所有顶点的数组（主表）。

2.每个顶点单独对应的链表，此链表包含了与此顶点相邻的所有顶点集合。

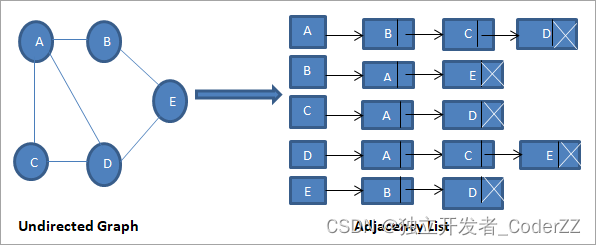
a.无向图的邻接表

b.有向图的邻接表

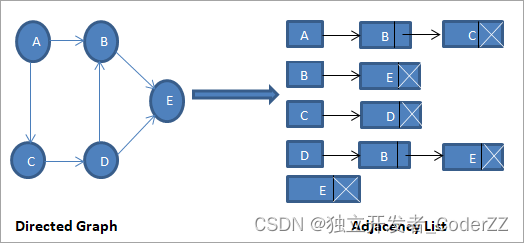
c.加权有向图的邻接表

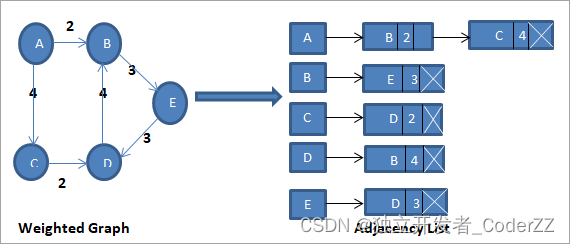
3.邻接表和邻接矩阵的对比

邻接矩阵的表示方式，简单直观且容易理解。其弱点在于，如果遇到了点很多而边很少的稀疏图，此时的矩阵包含大量的无效元素0，容易造成存储空间的浪费。

邻接表方便找任一顶点的所有邻接点，遇到稀疏图还能节省存储空间，其弱点在于，邻接表不方便检查任意两个顶点间是否存在边。

四，图的常见操作

由于邻接表的添加和删除操作比较容易，和链表结构的操作类似，此处主要展示邻接矩阵的添加和删除操作。

1.添加顶点

当添加一个顶点时，图形的大小会增加，从而使矩阵的行和列级别的大小加1。

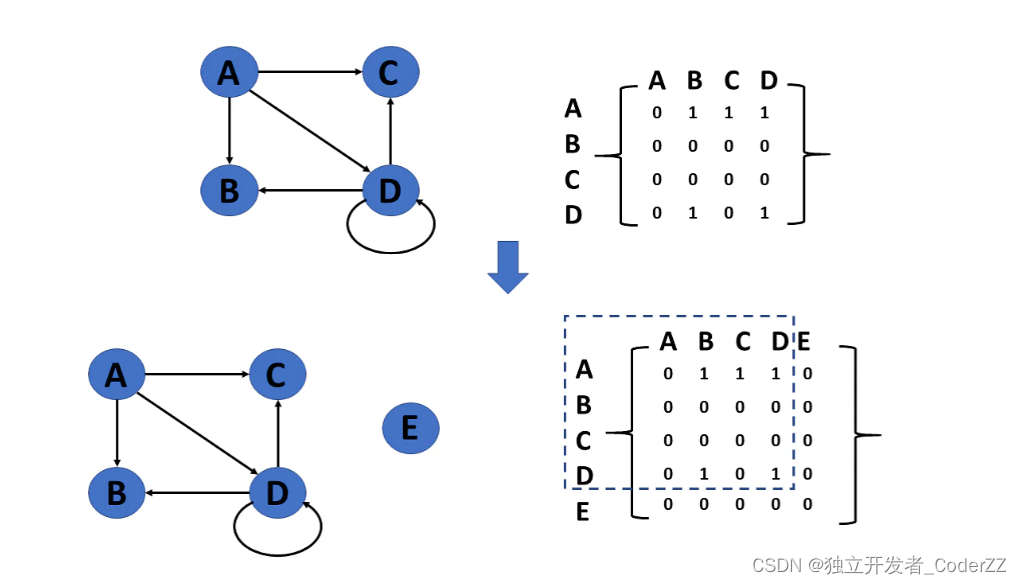
2.删除顶点

如果删除的顶点出现在图中，则矩阵返回该顶点。如果删除的顶点没有出现在图中，则不做任何操作，函数直接返回。删除完以后，矩阵的行和列级别的大小减1。

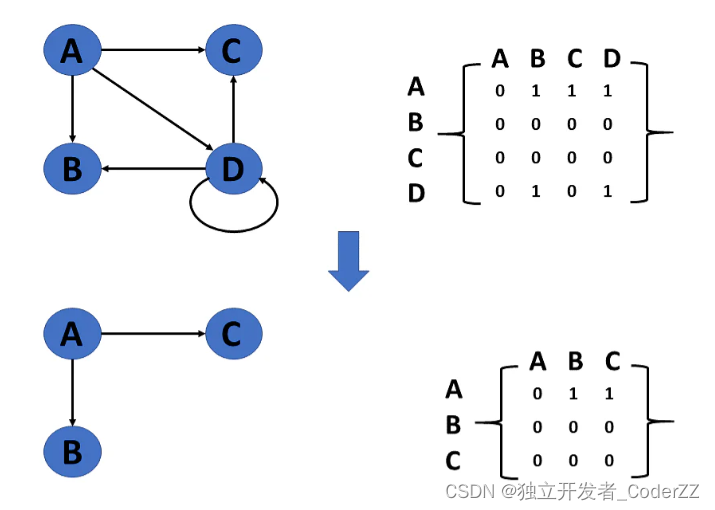
3.两个顶点之间添加边

在添加边之前，AdjMatrix(C, B)=0，在添加边以后，AdjMatrix(C, B)=1。

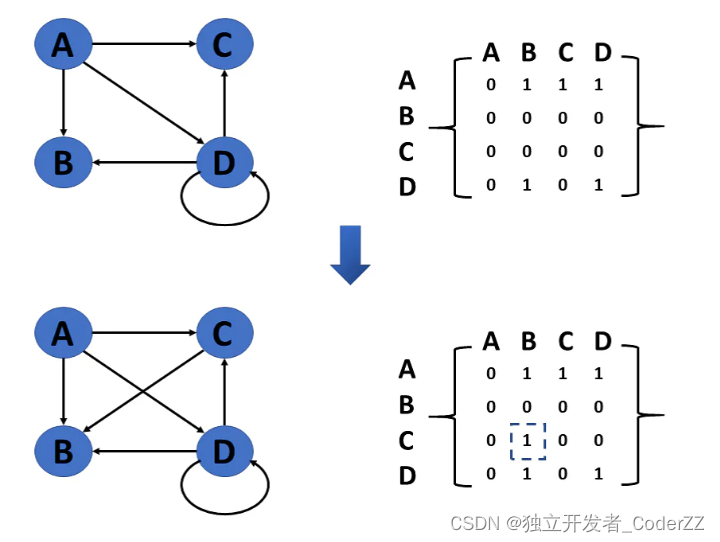
4.两个顶点之间删除边

在删除边之前，AdjMatrix(D, D)=1，在删除边以后，AdjMatrix(D, D)=0。

5.遍历

广度优先遍历(BFS)

广度优先遍历也可以说是层次遍历，它是逐层对元素进行访问的。

广度优先遍历从图的任意一个起始位置开始，将图按照深度进行切分(类似于树结构的分层)，在移动到下一个深度级别之前，先遍历当前深度级别的所有节点。

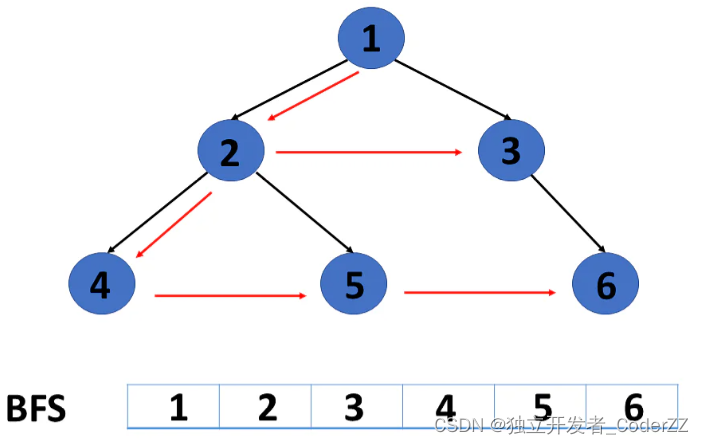
深度优先遍历(DFS)

深度优先是先任选一个出发点开始进行遍历，遍历的过程中，能继续往前移动就继续往前，如果不能就回退一步甚至再回退一步，然后从别的就近起点继续往前遍历。深度优先的遍历特点是，先选一条胡同走到底，走完了再跳到另外一条继续走到底。

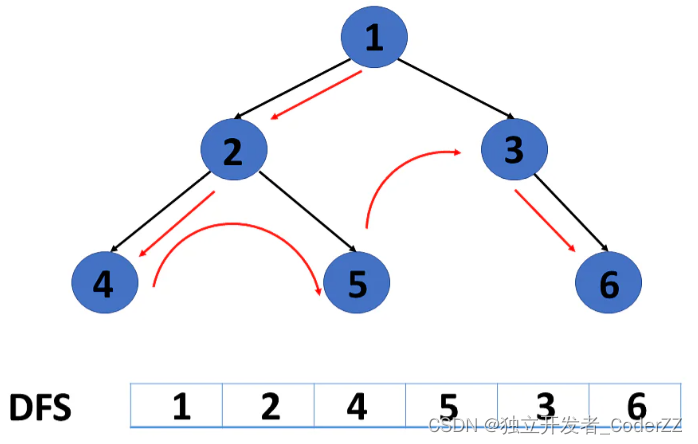
两种遍历方式的对比

深度优先遍历，在遍历的过程中不存储所有的结点，占用空间小，但是遍历过程中有回溯操作(入栈/出栈)，运行速度较慢。

广度优先遍历，在遍历的过程中存储所有的结点，占用空间大，但是无回溯操作，运行速度较快。

五，代码实例

1.邻接矩阵的代码样例

场景：

Python实现：

class Graph(object):
    def __init__(self, size):
        self.adjMatrix = []
        for i in range(size):
            self.adjMatrix.append([0 for i in range(size)])
        self.size = size

    def add_edge(self, v1, v2):
        if v1 == v2:
            print("Same vertex %d and %d" % (v1, v2))
        self.adjMatrix[v1][v2] = 1
        self.adjMatrix[v2][v1] = 1

    def remove_edge(self, v1, v2):
        if self.adjMatrix[v1][v2] == 0:
            print("No edge between %d and %d" % (v1, v2))
            return
        self.adjMatrix[v1][v2] = 0
        self.adjMatrix[v2][v1] = 0

    def __len__(self):
        return self.size

    def print_matrix(self):
        for row in self.adjMatrix:
            tmp = []
            for val in row:
                tmp.append(val)
            print(tmp)

def main():
    g = Graph(4)
    g.add_edge(0, 1)
    g.add_edge(0, 2)
    g.add_edge(1, 2)
    g.add_edge(0, 3)

    g.print_matrix()

if __name__ == '__main__':
    main()

运行结果：

[0, 1, 1, 1]
[1, 0, 1, 0]
[1, 1, 0, 0]
[1, 0, 0, 0]

C++实现：

#include <iostream>
using namespace std;
class Graph {
private:
    bool** adjMatrix;
    int numVertices;
public:
    Graph(int numVertices) {
        this->numVertices = numVertices;
        adjMatrix = new bool* [numVertices];
        for (int i = 0; i < numVertices; i++) {
            adjMatrix[i] = new bool[numVertices];
            for (int j = 0; j < numVertices; j++)
                adjMatrix[i][j] = false;
        }
    }

    void addEdge(int i, int j) {
        adjMatrix[i][j] = true;
        adjMatrix[j][i] = true;
    }

    void removeEdge(int i, int j) {
        adjMatrix[i][j] = false;
        adjMatrix[j][i] = false;
    }

    void toString() {
        for (int i = 0; i < numVertices; i++) {
            cout << i << " : ";
            for (int j = 0; j < numVertices; j++)
                cout << adjMatrix[i][j] << " ";
            cout << "\n";
        }
    }
    ~Graph() {
        for (int i = 0; i < numVertices; i++)
            delete[] adjMatrix[i];
        delete[] adjMatrix;
    }
};
int main() {
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(0, 3);
    g.toString();
}

运行结果：

0 : 0 1 1 1
1 : 1 0 1 0
2 : 1 1 0 0
3 : 1 0 0 0

2.邻接表的代码样例

场景：

6个顶点，9条边组成的加权有向图

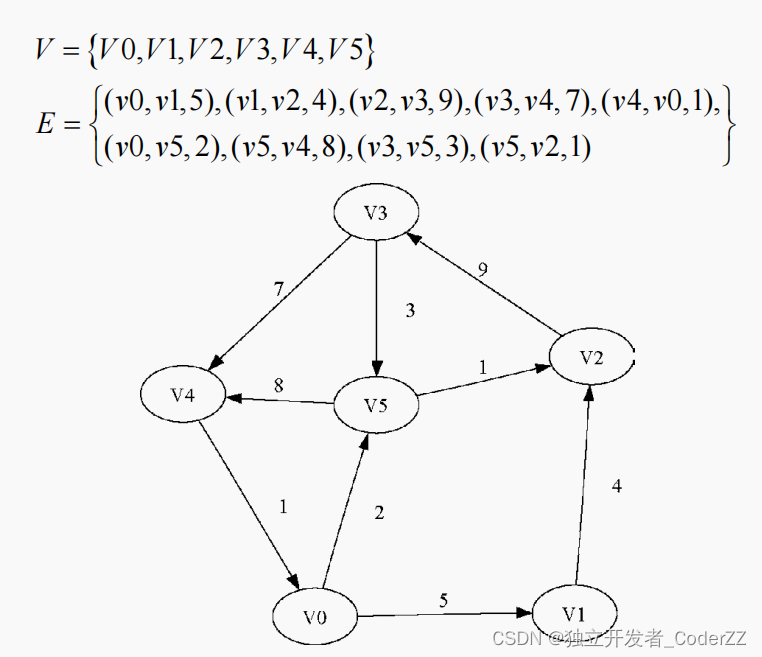
Python实现：

Python版的邻接矩阵，最简单的实现方式是为每个顶点都维护一个字典，字典的键是顶点，值是权重。

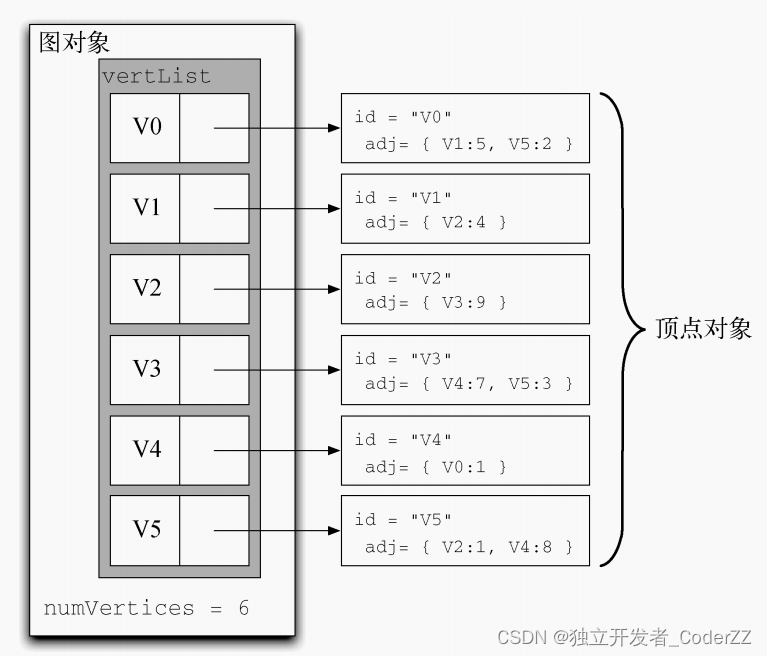
Graph类存储包含所有顶点的主列表。

Vertex类表示图中的每一个顶点，Vertex 使用字典 connectedTo 来记录与其相连的顶点，以及每一条边的权重。

class Graph:
    def __init__(self):
        self.vertList = {}
        self.numVertices = 0
    def addVertex(self, key):
        self.numVertices = self.numVertices + 1
        newVertex = Vertex(key)
        self.vertList[key] = newVertex
        return newVertex
    def getVertex(self, n):
        if n in self.vertList:
            return self.vertList[n]
        else:
            return None
    def __contains__(self, n):
        return n in self.vertList
    #向图中添加带权重的边
    def addEdge(self, f, t, cost=0):
        if f not in self.vertList:
            nv = self.addVertex(f)
        if t not in self.vertList:
            nv = self.addVertex(t)
        self.vertList[f].addNeighbor(self.vertList[t], cost)
    def getVertices(self):
        return self.vertList.keys()
    #魔法函数，遍历图中的所有顶点对象
    def __iter__(self):
        return iter(self.vertList.values())

class Vertex:
    def __init__(self, key):
        self.id = key
        self.connectedTo = {}
    def addNeighbor(self, nbr, weight=0):
        self.connectedTo[nbr] = weight
    def __str__(self):
        return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
    #返回邻接表中的所有顶点
    def getConnections(self):
        return self.connectedTo.keys()
    def getId(self):
        return self.id
    #返回指定顶点之间边上的权重
    def getWeight(self, nbr):
        return self.connectedTo[nbr]

if __name__ == '__main__':
    g = Graph()
    for i in range(6):
        g.addVertex(i)
    print("打印顶点对象: ", g.vertList)
    g.addEdge(0, 1, 5)
    g.addEdge(0, 5, 2)
    g.addEdge(1, 2, 4)
    g.addEdge(2, 3, 9)
    g.addEdge(3, 4, 7)
    g.addEdge(3, 5, 3)
    g.addEdge(4, 0, 1)
    g.addEdge(5, 4, 8)
    g.addEdge(5, 2, 1)
    for v in g:
        for w in v.getConnections():
            #遍历邻接表，返回顶点和邻接的顶点，以及边的权重
            print("( %s , %s : %s)" % (v.getId(), w.getId(), v.getWeight(w)))

运行结果：

打印顶点对象:  {0: <__main__.Vertex object at 0x0000013A5A55B358>,
1: <__main__.Vertex object at 0x0000013A5A55B390>,
2: <__main__.Vertex object at 0x0000013A5A55B3C8>,
3: <__main__.Vertex object at 0x0000013A5A55B400>,
4: <__main__.Vertex object at 0x0000013A5A55B438>,
5: <__main__.Vertex object at 0x0000013A5A55B470>}
( 0 , 1 : 5)
( 0 , 5 : 2)
( 1 , 2 : 4)
( 2 , 3 : 9)
( 3 , 4 : 7)
( 3 , 5 : 3)
( 4 , 0 : 1)
( 5 , 4 : 8)
( 5 , 2 : 1)

C++实现：

#include <iostream>
using namespace std;

struct adjNode {
    int val, cost;
    adjNode* next;
};
struct graphEdge {
    int start_ver, end_ver, weight;
};
class DiaGraph {
    adjNode* getAdjListNode(int value, int weight, adjNode* head) {
        adjNode* newNode = new adjNode;
        newNode->val = value;
        newNode->cost = weight;
        newNode->next = head;  
        return newNode;
    }
    int N;  
public:
    adjNode** head;                
    DiaGraph(graphEdge edges[], int n, int N) {
        head = new adjNode * [N]();
        this->N = N;
        for (int i = 0; i < N; ++i)
            head[i] = nullptr;
        for (unsigned i = 0; i < n; i++) {
            int start_ver = edges[i].start_ver;
            int end_ver = edges[i].end_ver;
            int weight = edges[i].weight;
            adjNode* newNode = getAdjListNode(end_ver, weight, head[start_ver]);
            head[start_ver] = newNode;
        }
    }
    ~DiaGraph() {
        for (int i = 0; i < N; i++)
            delete[] head[i];
        delete[] head;
    }
};

void display_AdjList(adjNode* ptr, int i)
{
    while (ptr != nullptr) {
        cout << "(" << i << ", " << ptr->val
            << ", " << ptr->cost << ") ";
        ptr = ptr->next;
    }
    cout << endl;
}

int main()
{
    // graph edges array.
    graphEdge edges[] = {
    // (x, y, w) -> edge from x to y with weight w
    {0, 1, 5},
    {0, 5, 2},
    {1, 2, 4},
    {2, 3, 9},
    {3, 4, 7},
    {3, 5, 3},
    {4, 0, 1},
    {5, 4, 8},
    {5, 2, 1}
    };
    int N = 6;  // Number of vertices in the graph                                      
    int n = sizeof(edges) / sizeof(edges[0]); // calculate number of edges
    DiaGraph diagraph(edges, n, N);
    cout << "Graph adjacency list " << endl << "(start_vertex, end_vertex, weight):"  << endl;
    for (int i = 0; i < N; i++)
    {
        display_AdjList(diagraph.head[i], i);
    }
    return 0;
}

运行结果：

Graph adjacency list
(start_vertex, end_vertex, weight):
(0, 5, 2) (0, 1, 5)
(1, 2, 4)
(2, 3, 9)
(3, 5, 3) (3, 4, 7)
(4, 0, 1)
(5, 2, 1) (5, 4, 8)

3.广度优先的代码样例

场景： 

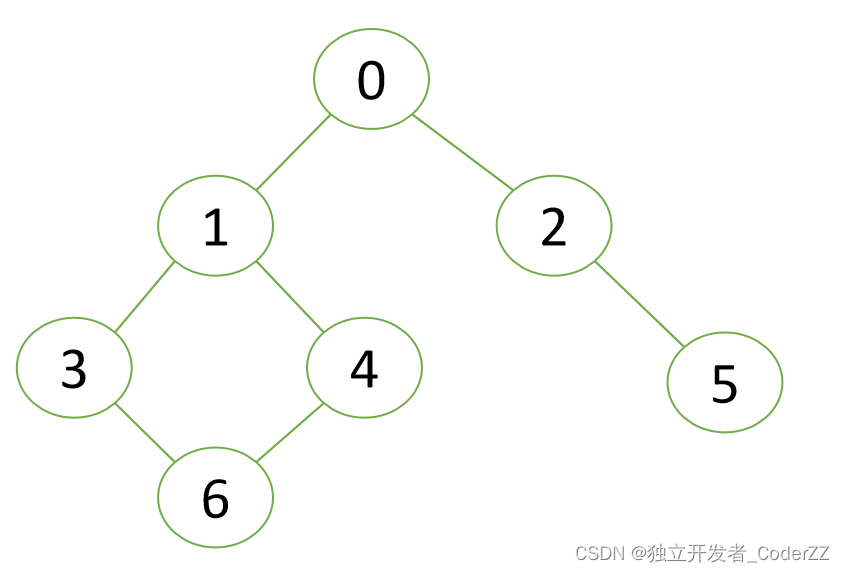
遍历顺序： 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6

Python实现：

class Graph:
    adj = []
    def __init__(self, v, e):
        self.v = v
        self.e = e
        Graph.adj = [[0 for i in range(v)]
                     for j in range(v)]

    def addEdge(self, start, e):
        Graph.adj[start][e] = 1
        Graph.adj[e][start] = 1

    def BFS(self, start):
        visited = [False] * self.v
        q = [start]

        # Set source as visited
        visited[start] = True

        while q:
            vis = q[0]

            # Print current node
            print(vis, end=' ')
            q.pop(0)

            # For every adjacent vertex to
            # the current vertex
            for i in range(self.v):
                if (Graph.adj[vis][i] == 1 and
                        (not visited[i])):
                    # Push the adjacent node
                    # in the queue
                    q.append(i)
                    visited[i] = True

v, e = 7, 7

#Create the graph
G = Graph(v, e)
G.addEdge(0, 1)
G.addEdge(0, 2)
G.addEdge(1, 3)
G.addEdge(1, 4)
G.addEdge(2, 5)
G.addEdge(6, 3)
G.addEdge(6, 4)

G.BFS(0)

运行结果：

0 1 2 3 4 5 6

C++实现：

#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> adj;

void addEdge(int x, int y)
{
       adj[x][y] = 1;
       adj[y][x] = 1;
}

void bfs(int start)
{
       vector<bool> visited(adj.size(), false);
       vector<int> q;
       q.push_back(start);
       // Set source as visited
       visited[start] = true;
       int vis;
       while (!q.empty()) {
              vis = q[0];
              // Print the current node
              cout << vis << " ";
              q.erase(q.begin());
              // For every adjacent vertex to the current vertex
              for (int i = 0; i < adj[vis].size(); i++) {
                      if (adj[vis][i] == 1 && (!visited[i])) {
                             // Push the adjacent node to the queue
                             q.push_back(i);
                             // Set
                             visited[i] = true;
                      }
              }
       }
}

int main()
{
       // number of vertices
       int v = 7;
       // adjacency matrix
       adj = vector<vector<int>>(v, vector<int>(v, 0));
       addEdge(0, 1);
       addEdge(0, 2);
       addEdge(1, 3);
       addEdge(1, 4);
       addEdge(2, 5);
       addEdge(6, 3);
       addEdge(6, 4);

       bfs(0);
}

运行结果：

0 1 2 3 4 5 6

4.深度优先的代码样例

场景:

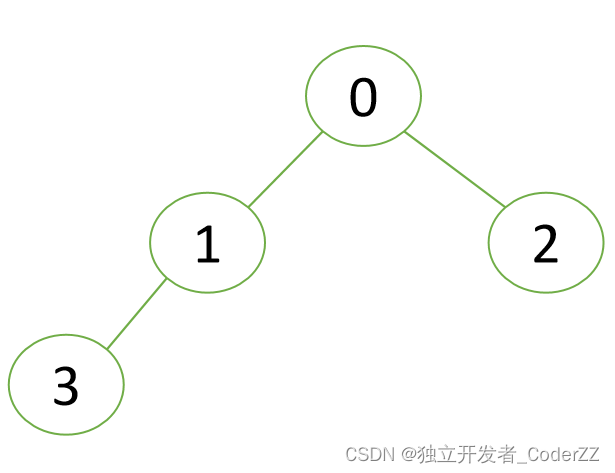
遍历顺序：0 -> 1 -> 3 -> 2

Python实现：

class Graph:
    adj = []

    def __init__(self, v, e):
        self.v = v
        self.e = e
        Graph.adj = [[0 for i in range(v)]
                     for j in range(v)]

    def addEdge(self, start, e):
        Graph.adj[start][e] = 1
        Graph.adj[e][start] = 1

    def DFS(self, start, visited):
        print(start, end=' ')
        visited[start] = True
        for i in range(self.v):
            if (Graph.adj[start][i] == 1 and
                    (not visited[i])):
                self.DFS(i, visited)

v, e = 5, 4

G = Graph(v, e)
G.addEdge(0, 1)
G.addEdge(0, 2)
G.addEdge(1, 3)

G.DFS(0, visited);

运行结果：

0 1 3 2

C++实现：

#include <bits/stdc++.h>
using namespace std;

vector<vector<int> > adj;
void addEdge(int x, int y)
{
       adj[x][y] = 1;
       adj[y][x] = 1;
}
void dfs(int start, vector<bool>& visited)
{
       // Print the current node
       cout << start << " ";
       // Set current node as visited
       visited[start] = true;
       // For every node of the graph
       for (int i = 0; i < adj[start].size(); i++) {
              // If some node is adjacent to the current node
              // and it has not already been visited
              if (adj[start][i] == 1 && (!visited[i])) {
                      dfs(i, visited);
              }
       }
}
int main()
{
       // number of vertices
       int v = 5;
       // number of edges
       int e = 4;
       // adjacency matrix
       adj = vector<vector<int> >(v, vector<int>(v, 0));
       addEdge(0, 1);
       addEdge(0, 2);
       addEdge(1, 3);
       vector<bool> visited(v, false);

       dfs(0, visited);
}

运行结果：

0 1 3 2

六，参考阅读

《Problem Solving with Algorithms and Data Structures Using Python, Second Edition》

https://www.simplilearn.com/tutorials/data-structure-tutorial/graphs-in-data-structure

https://www.softwaretestinghelp.com/graph-implementation-cpp/

https://www.programiz.com/dsa/graph-adjacency-matrix

https://www.geeksforgeeks.org/implementation-of-dfs-using-adjacency-matrix/

https://www.geeksforgeeks.org/implementation-of-bfs-using-adjacency-matrix/

https://www.programiz.com/dsa/graph-adjacency-matrix