快速傅里叶变换（FFT）——按时间抽取DIT的基-CFANZ编程社区

【1】前言

1、DIF计算量

快速傅里叶变换（FFT）——按时间抽取DIT的基_数位
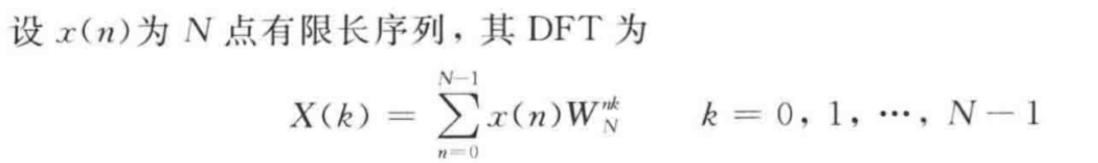
更加清楚地了解计算步骤：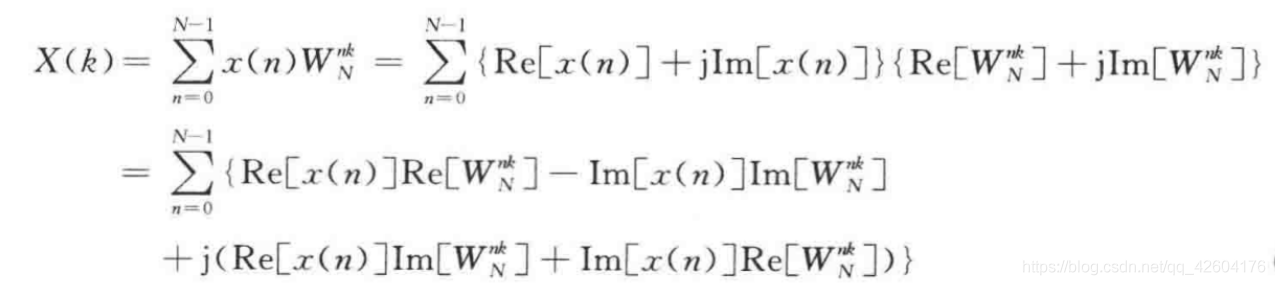
快速傅里叶变换（FFT）——按时间抽取DIT的基_倒序_02
观察可知：
1、一次复数乘法需用四次实数乘法和二次实数加法；
2、一次复数加法需二次实数加法
3、整个 DFT 运算总共需要 4N^2 次实数乘法和 2N*(2N—1)次实数加法。
总结：
直接计算 DFT,乘法次数和加法次数都是和 N^2 成正比的。

2、利用性质改善

快速傅里叶变换（FFT）——按时间抽取DIT的基_倒序_03
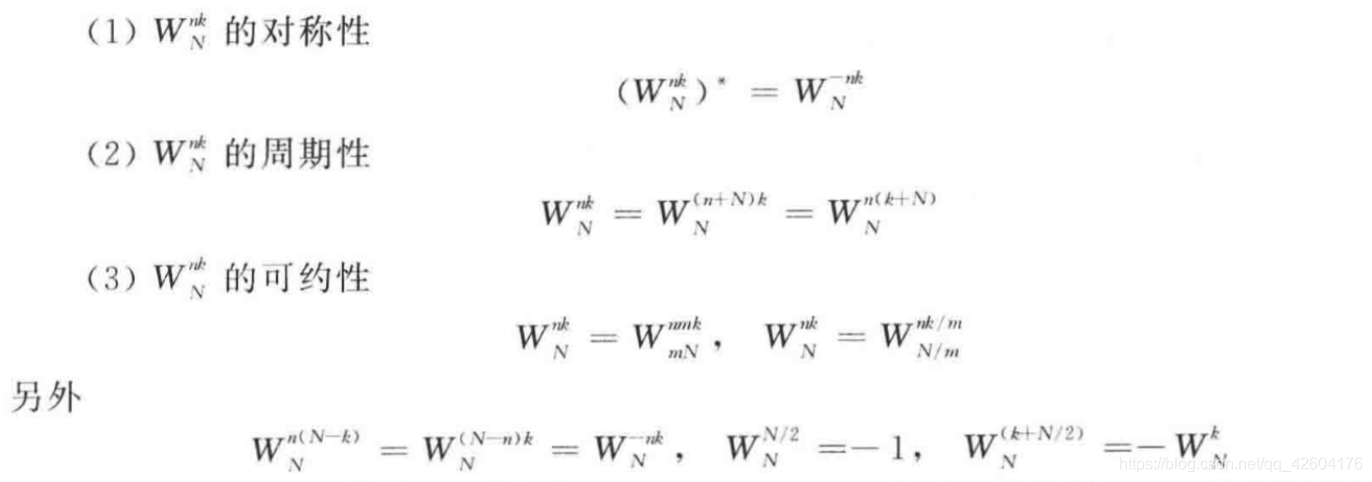
利用这些性质，将较大的N分解为若干个较小的N然后进行运算。

【2】公式推导

1、N 到 2*N/2

a、分解原序列

快速傅里叶变换（FFT）——按时间抽取DIT的基_倒序_04

b、分解后的DFT变换

快速傅里叶变换（FFT）——按时间抽取DIT的基_算法_05
快速傅里叶变换（FFT）——按时间抽取DIT的基_数位_06

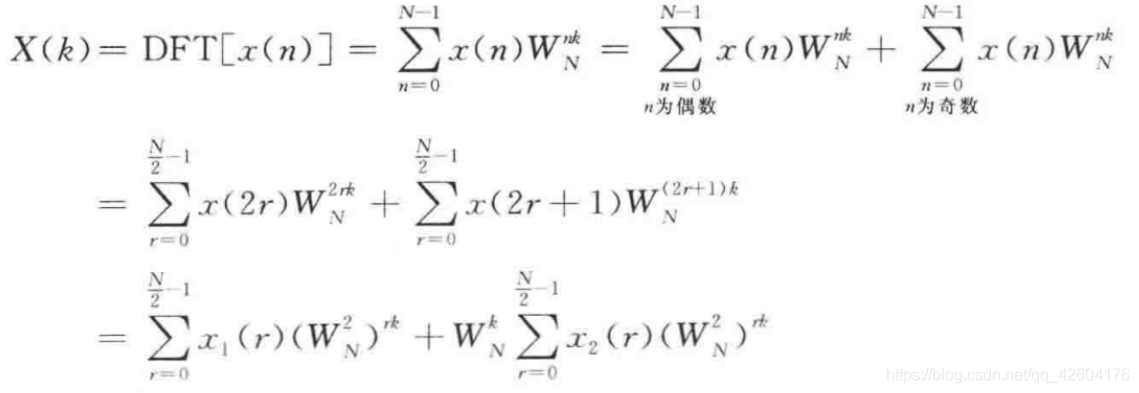
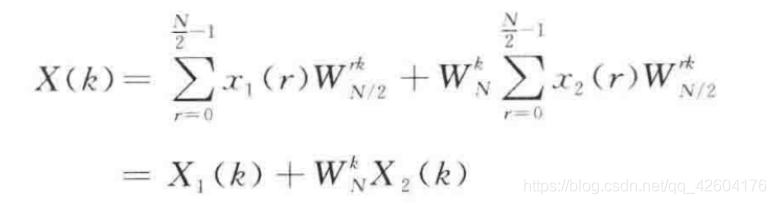
c、一系列化简操作之后

快速傅里叶变换（FFT）——按时间抽取DIT的基_算法_07

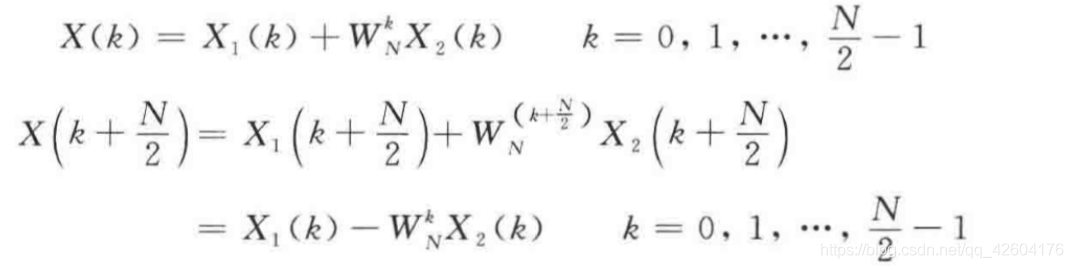
d、蝶形信号流

快速傅里叶变换（FFT）——按时间抽取DIT的基_倒序_08
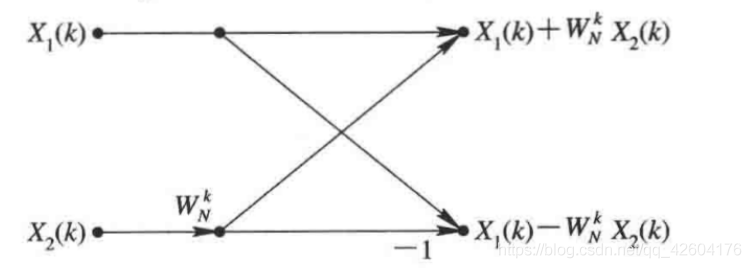
以N=8的序列为例：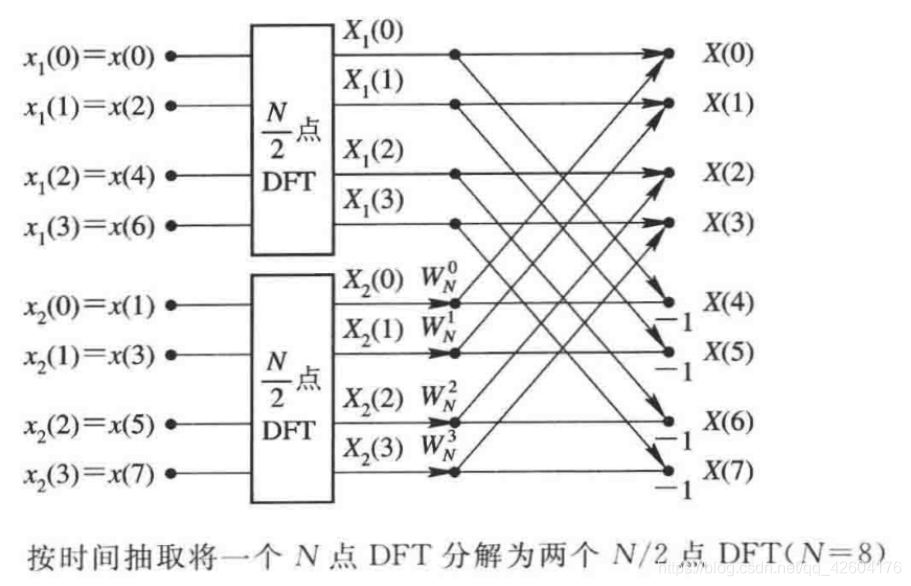
快速傅里叶变换（FFT）——按时间抽取DIT的基_倒序_09

e、计算量总结

因而通过第一步分解后，总共需要（N^2/2)+(N/2)=N(N+l )/2约等于 N^2/2 次复数乘法和 N( N/2-1 )+N = N^2/2 次复数加法。由此可见，通过这样分解后的运算工作量差不多节省了一半。

2、N/2 到 2*N/4

a、分解X2(k)序列

快速傅里叶变换（FFT）——按时间抽取DIT的基_倒序_10

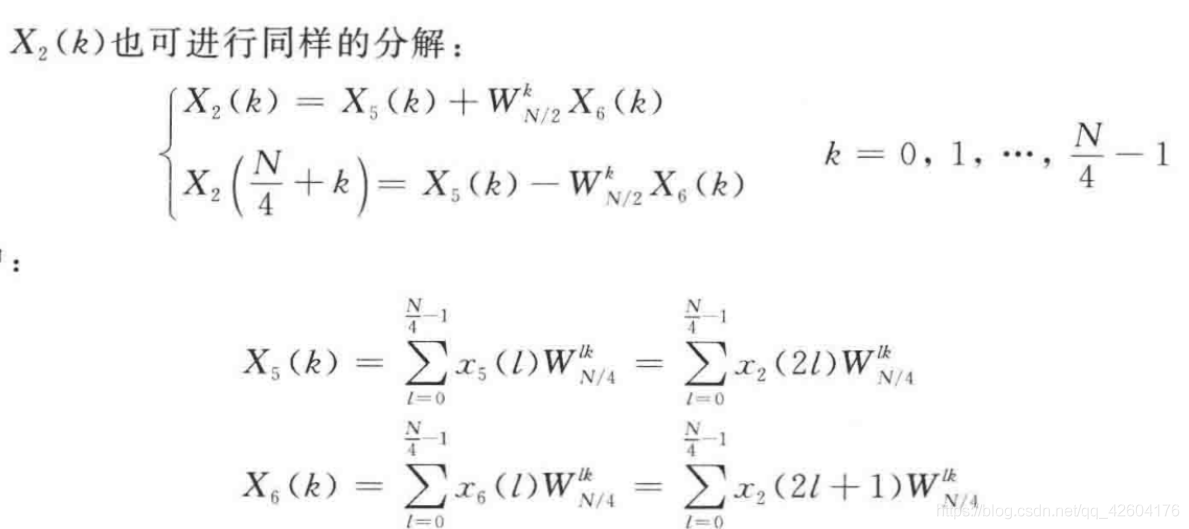
b、蝶形信号流（2列）

快速傅里叶变换（FFT）——按时间抽取DIT的基_数位_11

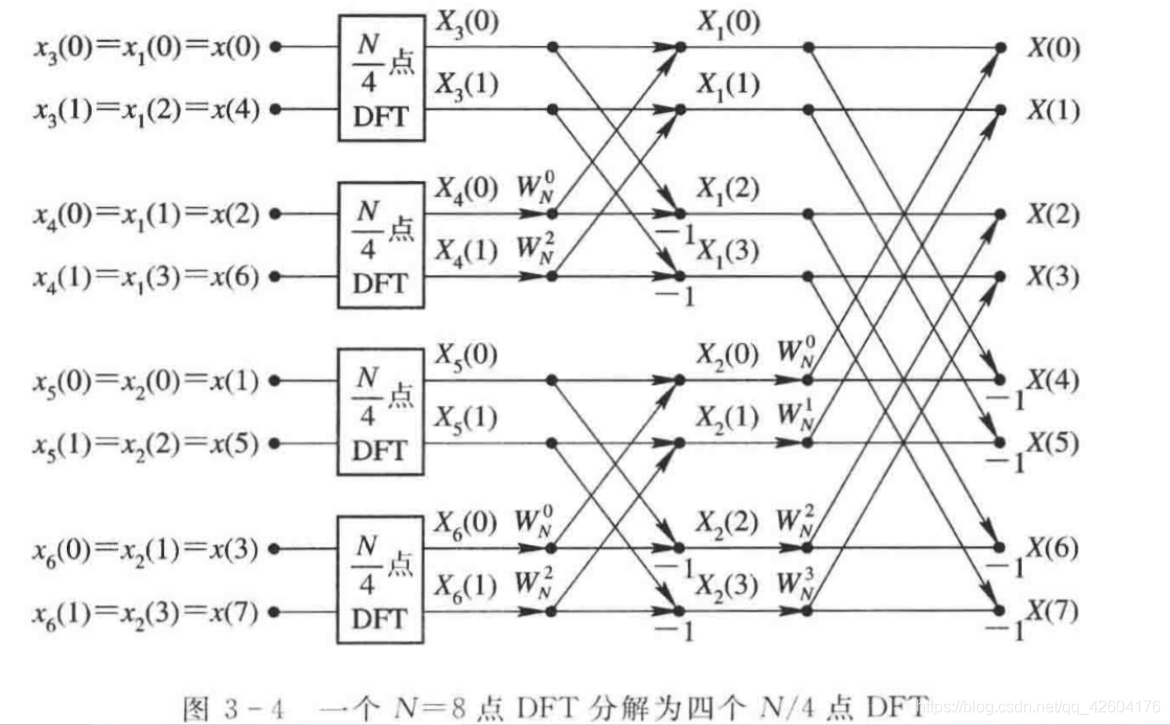
3、N/4 到 2*N/8

a、蝶形信号流（3列）

快速傅里叶变换（FFT）——按时间抽取DIT的基_算法_12

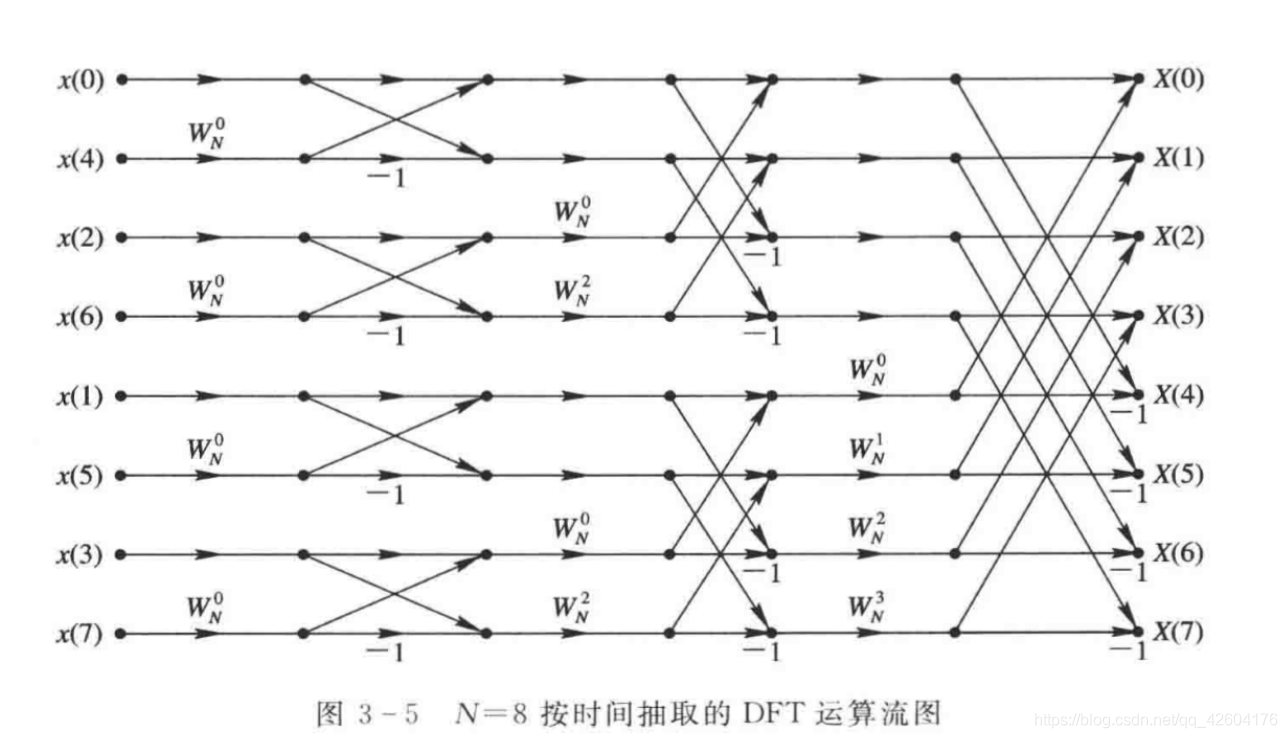
【3】公式总结

由于乘法的运算量较大，我们从乘法角度来探讨一下，DFT和FFT的运算量。
设N=2^M；有M列的蝶形信号运算。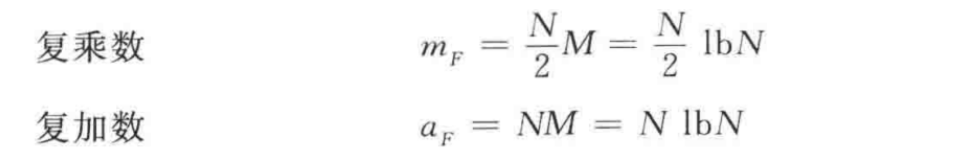
快速傅里叶变换（FFT）——按时间抽取DIT的基_二进制数_13
从乘法角度：DFT需要N^2,FFT需要N*lbN;

当N=2048时，这一比值为372.4,即直接计算DFT的运算量是FFT运算量的372.4倍。
当点数N越大时，FFT的优点更为明显。

【4】特点以及程序框架讲解

1、原址运算

快速傅里叶变换（FFT）——按时间抽取DIT的基_算法_15
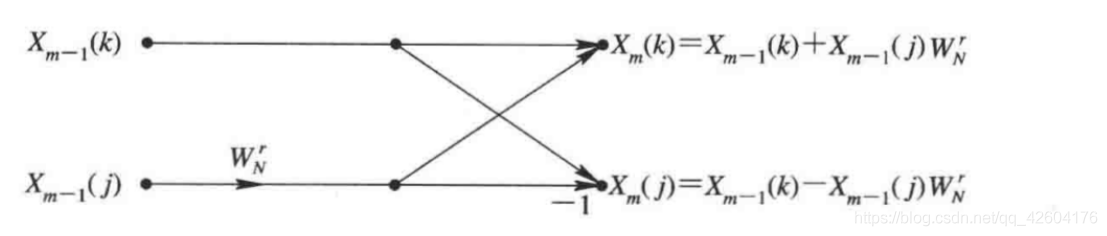
计算之后，将新的X(k)覆盖原本的X(k)。
注意：是将同一行的X进行覆盖（后面的列覆盖前面的列），不同行之间是没有覆盖关系的。
所以，最后只需要N个存储单元。（N个数据,N行）

2、倒位序规律

输出X(k),序列正常。
输入序列不正常。
原因：X(n)按照标号n的奇偶而不断分组。
例子：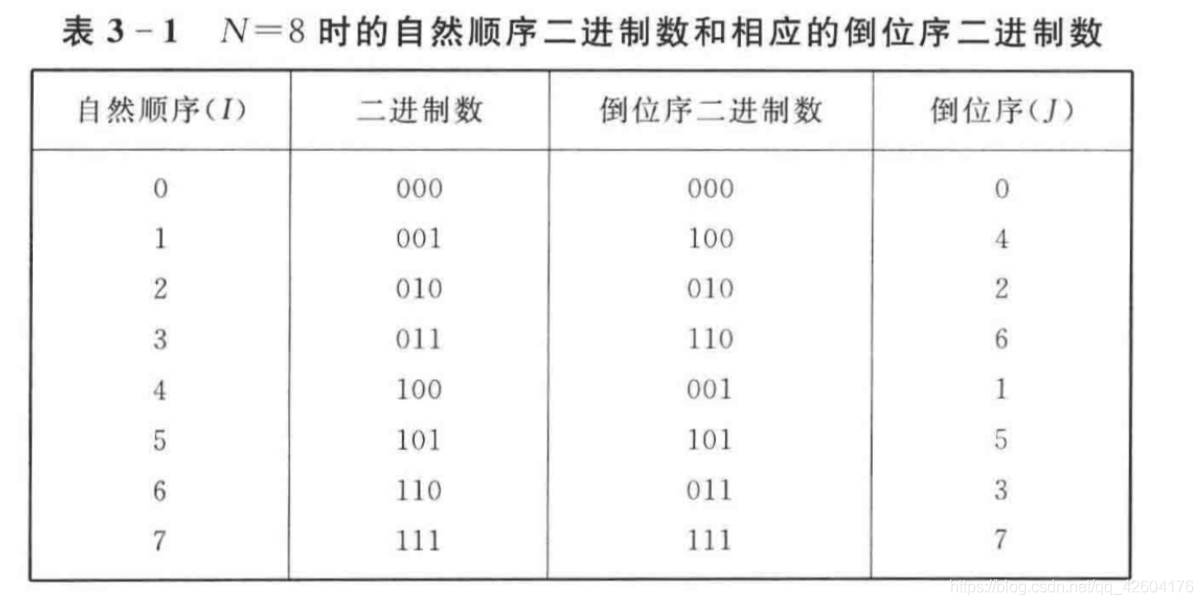
快速傅里叶变换（FFT）——按时间抽取DIT的基_倒序_16
步骤流程：
I+1，最低位+1，向左进位。
J在二进制最高位+1，逢2向右进位。
由此可以从当前的倒序值计算求得下一个倒序值。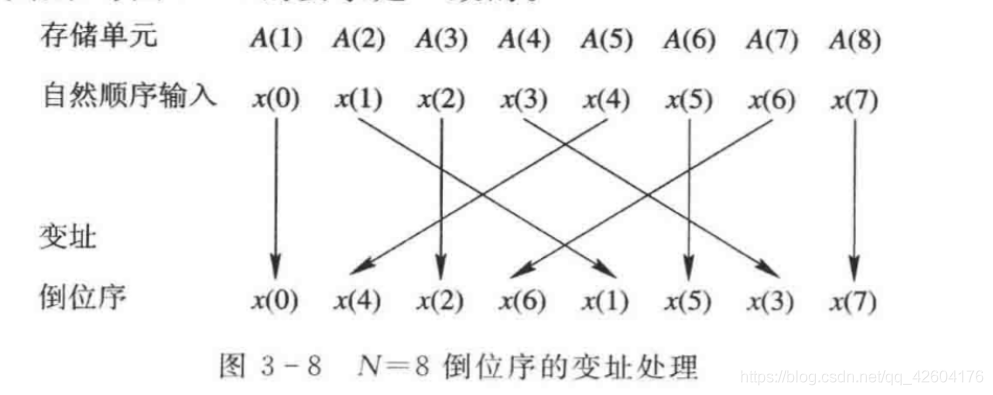
快速傅里叶变换（FFT）——按时间抽取DIT的基_二进制数_17
观察变址处理，可以发现，只有当J>I时，才将X(I)和X(J)存储内容进行互换。

3、蝶形运算两节点的距离

输入为倒位序，输出为正位序，N=2^ M,在第m级运算，两个节点间的距离为2^(m-1);

4、WN^r的确定

r的变换规律：
1、运算两个节点中第一个节点标号为k，表示为M位的二进制数。
2、将此二进制数乘以2^(M-m)，相当于左移M-m位，把右边空出，此数位r的二进制数。

5、程序框架

快速傅里叶变换（FFT）——按时间抽取DIT的基_数位_18

【5】代码实现

没有验证代码的正确性，只是按照上面的流程图进行叙述。

#define PI 3.14159


//数位倒读
int rev(int i, int m) {//i=0~2^m,m为二进制位数 
  int j = 0;
  while (m > 0) {
    j += (i & 0x01) * (0x01 << (m - 1));//j+=(i%2)*mypow(2,m-1);
    i >>= 1;//i/=2
    m -= 1;
  }
  return j;
}

//快速傅里叶变换
//输入x(n)、N
//输出X(k)
void fft(const float real_in[], const float imag_in[], float real_out[], float imag_out[],int N) 
{
  //【1】获取M
  int M = log2(N);  
  //【2】倒序
  for (int i = 0;i < N;i++) 
  {//数位倒读 
    int j;
    j = rev(i, M);
    real_out[j] = real_in[i];
    imag_out[j] = imag_in[i];
  }
  //【3】
  for (int m = 1;m <= M;m++)
  {
    int B = 2 ^ m - 1;
    for (int J = 0;J <= B - 1;J++)
    {
      int P = 2 ^ (M - m) * J;
      for (int k = J;k <= N - 1;k++)
      {
        float tmpr1, tmpi1, tmpr2, tmpi2;//临时变量
        float theta = -2 * PI * P / N ;
        tmpr1 = real_out[k];
        tmpi1 = imag_out[k];
        tmpr2 = cos(theta) * real_out[k + B] - sin(theta) * imag_out[k + B];
        tmpi2 = cos(theta) * imag_out[k + B] + sin(theta) * real_out[k + B];
        real_out[k] = tmpr1 + tmpr2;
        imag_out[k] = tmpi1 + tmpi2;
        real_out[k + B] = tmpr1 - tmpr2;
        imag_out[k + B] = tmpi1 - tmpi2;
      }

    }

  }
}