📌📌📌为您导航📌📌📌

• 1.二叉搜索树概念
• 2.二叉搜索树非递归实现
• • 2.1初始结构定义
  • 2.2二叉搜索树插入
  • 2.3二叉搜索树查找
  • 2.4二叉搜索树删除
  • 2.5二叉搜索树中序遍历
• 3.二叉搜索树递归实现
• • 3.1二叉搜索树插入
  • 3.2二叉搜索树查找
  • 3.3二叉搜索树删除
• 4.key-value版本二叉搜索树

1.二叉搜索树概念

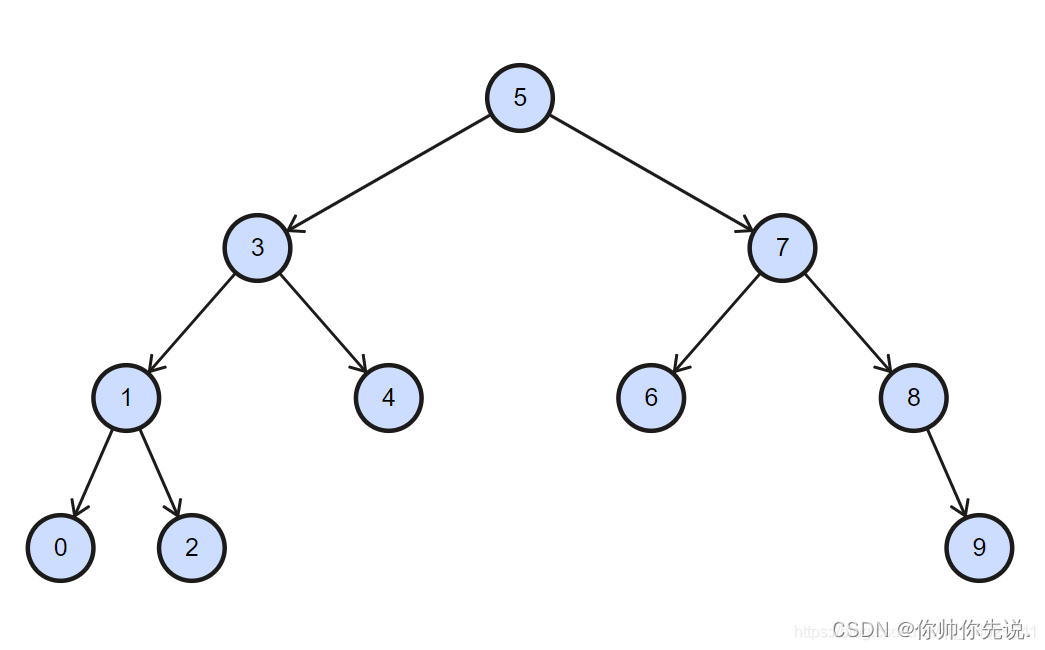
2.二叉搜索树非递归实现

2.1初始结构定义

template<class K>
struct BSTreeNode
{
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;
	//构造函数
	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

2.2二叉搜索树插入

bool Insert(const K& key)
{
	//空树,创建根结点
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	
	Node* parent = nullptr;
	Node* cur = _root;
	//寻找待插入结点的位置
	while (cur)
	{
		//如果待插入结点比cur指向的结点大,则去该结点的右边去找
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		//如果待插入结点比cur指向的结点小,则去该结点的左边去找
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		//二叉搜索树不允许有重复的值。
		else
		{
			return false;
		}
	}
	//走到这里说明找到插入的位置了,可以创建结点进行插入
	cur = new Node(key);
	//如果比父结点大,则在其右边插入
	if (parent->_key < key)
	{
		parent->_right = cur;
	}
	//如果比父结点小,则在其左边插入
	else
	{
		parent->_left = cur;
	}

	return true;
}

2.3二叉搜索树查找

bool Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		//如果cur的key值比key小,则在其右边查找
		if (cur->_key < key)
		{
			cur = cur->_right;
		}
		//如果cur的key值比key大,则在其左边查找
		else if (cur->_key > key)
		{
			cur = cur->_left;
		}
		//找到key值,返回true
		else
		{
			return true;
		}
	}
	//走到这说明没找到,返回false
	return false;
}

2.4二叉搜索树删除

bool Erase(const K& key)
{
	Node* parent = nullptr;
	Node* cur = _root;

	while (cur)
	{
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			// 找到，准备开始删除,所有情况的图解均在代码段下
			if (cur->_left == nullptr)
			{	//此种情况对应图1
				if (parent == nullptr)
				{
					_root = cur->_right;
				}
				else
				{   //此种情况对应图2
					if (parent->_left == cur)
						parent->_left = cur->_right;
					else
						parent->_right = cur->_right;
				}

				delete cur;
			}
			//此种情况和上面的类似
			else if (cur->_right == nullptr)
			{
				if (parent == nullptr)
				{
					_root = cur->_left;
				}
				else
				{
					if (parent->_left == cur)
						parent->_left = cur->_left;
					else
						parent->_right = cur->_left;
				}

				delete cur;
			}
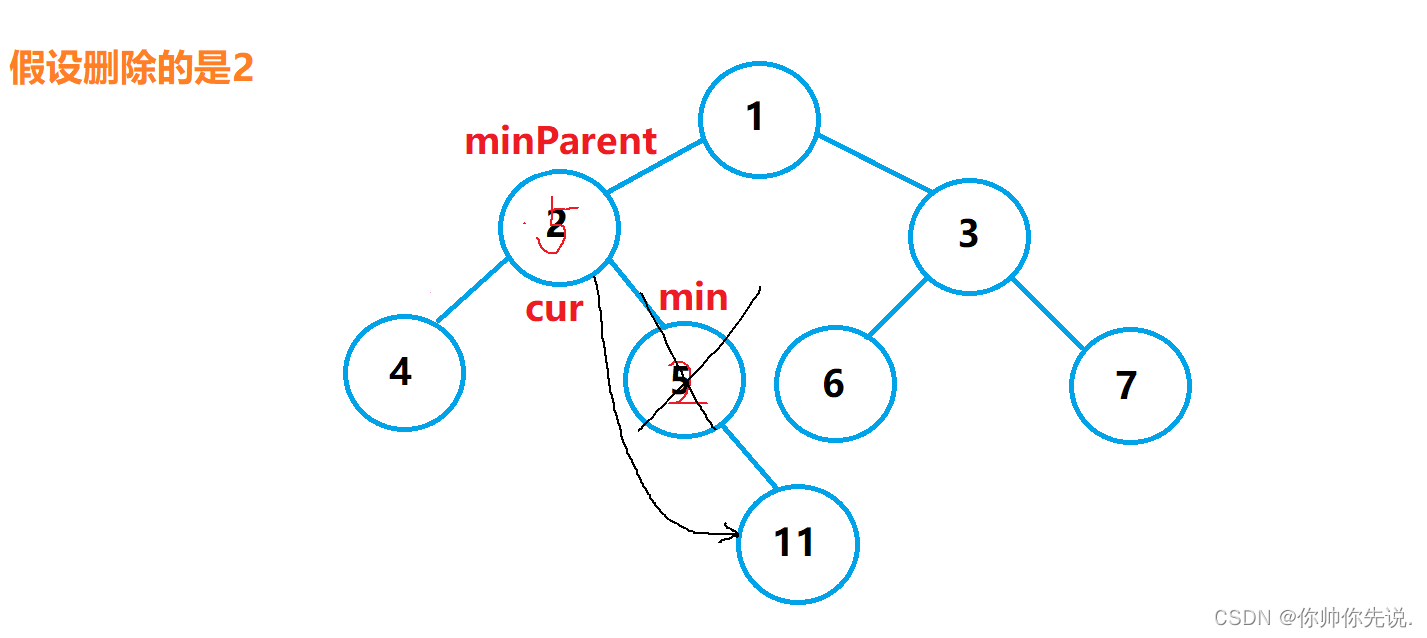
			//走到这说明左右都不为空
			else
			{
				Node* minParent = cur;
				Node* min = cur->_right;
				while (min->_left)
				{
					minParent = min;
					min = min->_left;
				}

				cur->_key = min->_key;
				//此种情况对应图3
				if (minParent->_left == min)
					minParent->_left = min->_right;
				else
					minParent->_right = min->_right;

				delete min;
			}

			return true;
		}
	}

	return false;
}

图1

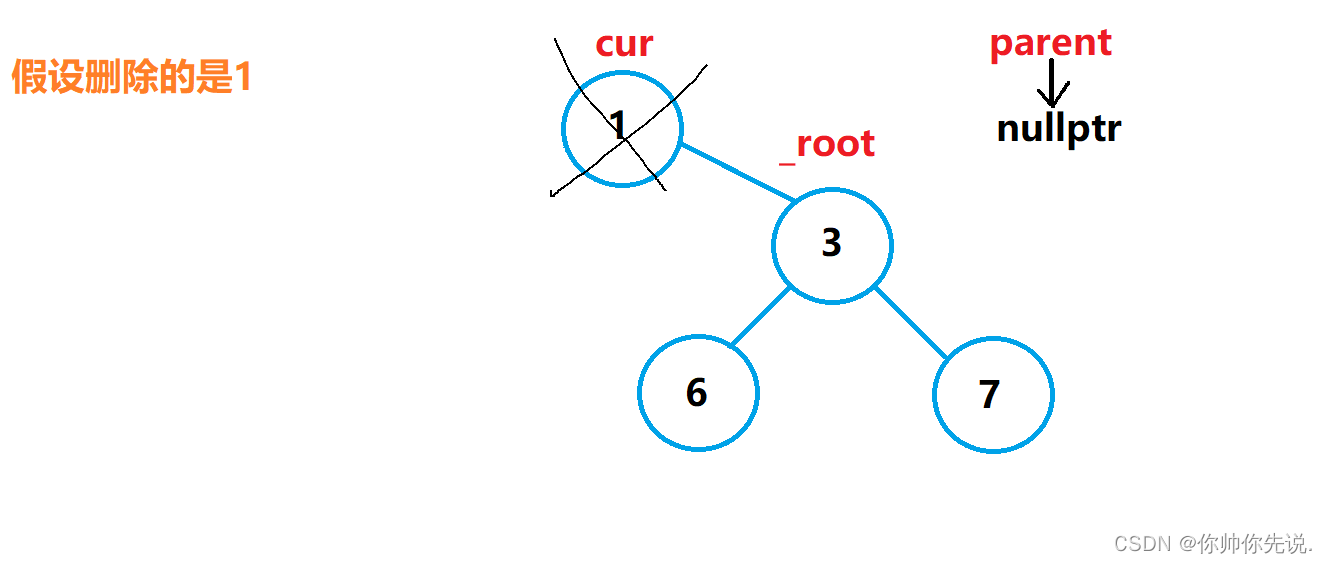
图2


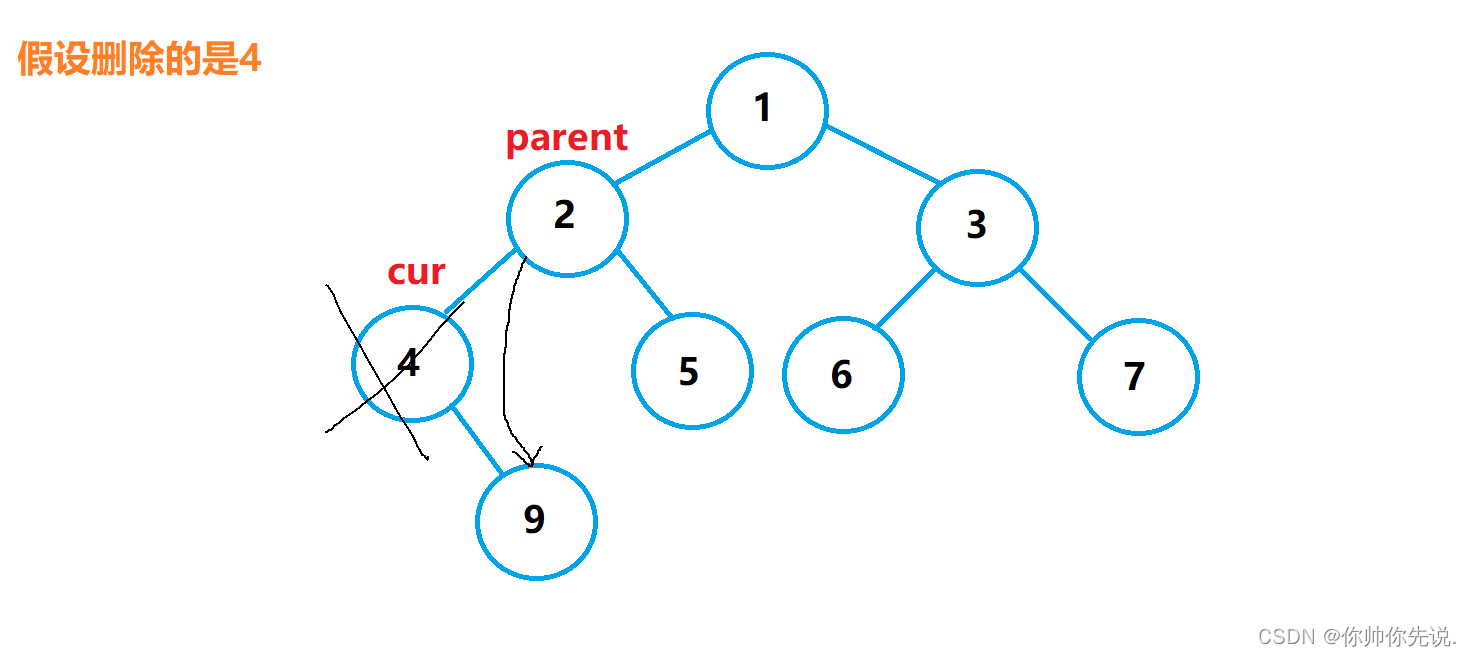
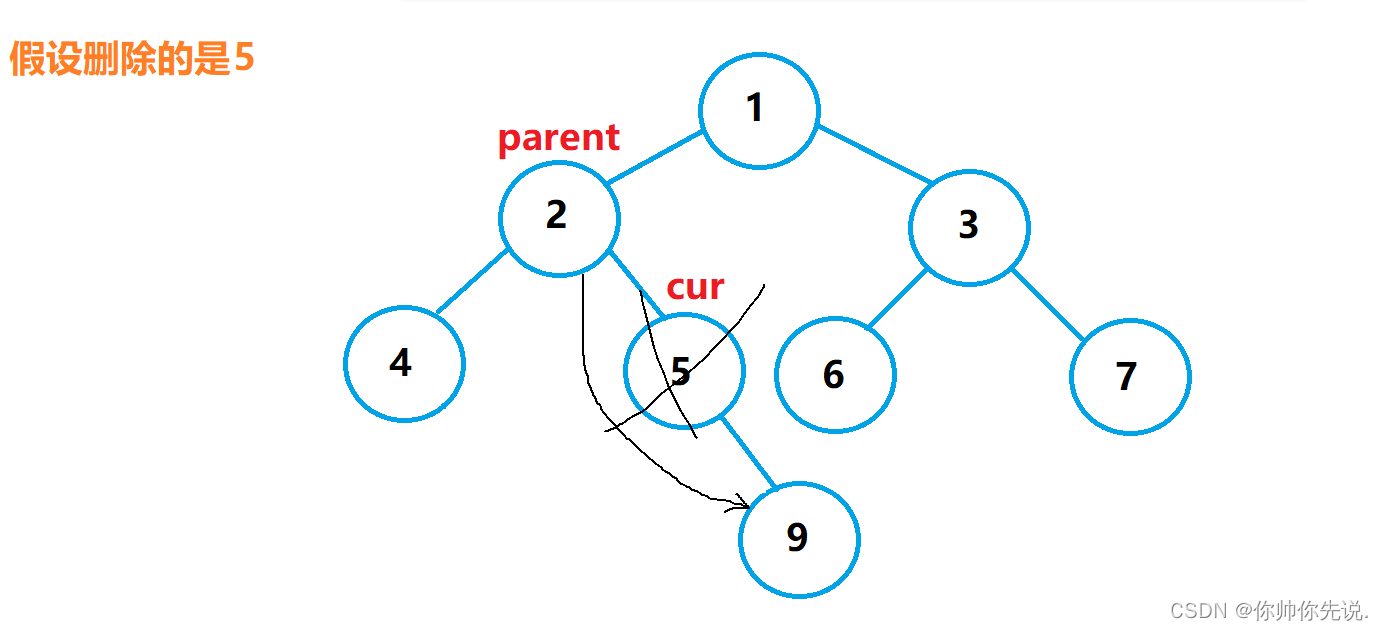
图3

2.5二叉搜索树中序遍历

public:
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
private:
	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		 //左子树
		_InOrder(root->_left);
		//根
		cout << root->_key << " ";
		//右子树
		_InOrder(root->_right);
	}

这里解释一下这边为什么要用这种写法，因为_root是私有类型，所以就没办法作为参数传递，所以我们就用一个子函数来作为输出型参数。
就比如这样

void InOrder(Node* root)
{
	if (root == nullptr)
	{
		return;
	}
	InOrder(root->_left);
	cout << root->_key << " ";
	InOrder(root->_right);
}

要调用此函数就一定得传根结点，根结点又是私有的，所以用上面的方法可以解决。

3.二叉搜索树递归实现

3.1二叉搜索树插入

public:
	bool InsertR(const K& key)
	{
		return _InsertR(_root, key);
	}
private:
	bool _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			root = new Node(key);
			return true;
		}
		//key值比当前结点大，则从此结点右树寻找
		if (root->_key < key)
			return _InsertR(root->_right, key);
		//key值比当前结点小，则从此结点左树寻找
		else if (root->_key > key)
			return _InsertR(root->_left, key);
		//相等，则插入失败
		else
			return false;
	}

3.2二叉搜索树查找

public:
	Node* FindR(const K& key)
	{
		return _FindR(_root, key);
	}
private:
	Node* _FindR(Node* root, const K& key)
	{
		if (root == nullptr)
		{
			return nullptr;
		}
		//key值比当前结点大，则从此结点右树寻找
		if (root->_key < key)
		{
			return _FindR(root->_right, key);
		}
		//key值比当前结点小，则从此结点左树寻找
		else if (root->_key > key)
		{
			return _FindR(root->_left, key);
		}
		//相等，则查找成功
		else
		{
			return root;
		}
	}

3.3二叉搜索树删除

public:
	bool EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}
private:
	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;
		//key值比当前结点大，则从此结点右树寻找
		if (root->_key < key)
		{
			return _EraseR(root->_right, key);
		}
		//key值比当前结点小，则从此结点左树寻找
		else if (root->_key > key)
		{
			return _EraseR(root->_left, key);
		}
		//此时开始删结点
		else
		{
			Node* del = root;
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			}
			else
			{
				Node* min = root->_right;
				while (min->_left)
				{
					min = min->_left;
				}

				swap(min->_key, root->_key);

				return _EraseR(root->_right, key);
			}
			delete del;
			
			return true;
		}
	}

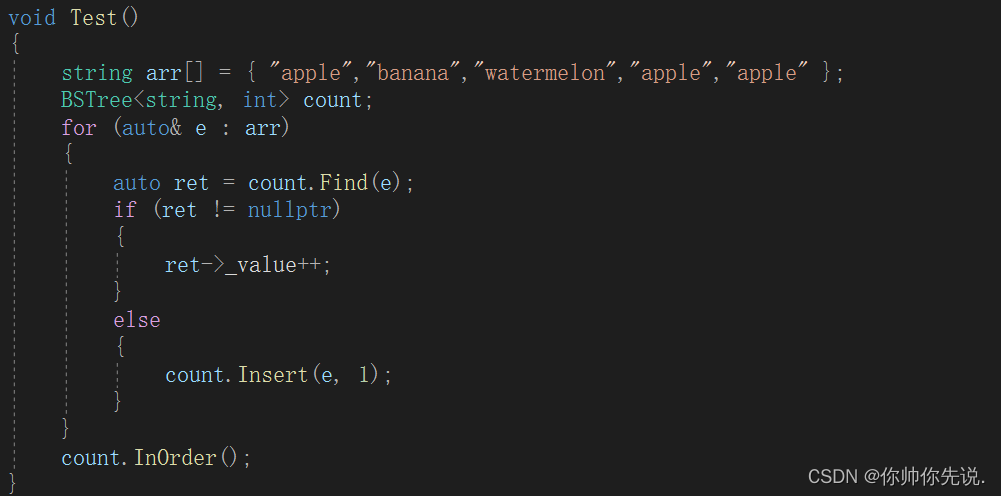
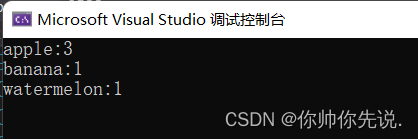
4.key-value版本二叉搜索树

实际上这个版本的二叉搜索树只要在原来代码的基础上加一个value值然后对初始化和插入做修改即可。

namespace KV
{
	template<class K, class V>
	struct BSTreeNode
	{
		BSTreeNode<K, V>* _left;
		BSTreeNode<K, V>* _right;
		K _key;
		V _value;


		BSTreeNode(const K& key, const V& value)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			, _value(value)
		{}
	};

	template<class K, class V>
	struct BSTree
	{
		typedef BSTreeNode<K, V> Node;
	public:
		BSTree()
			:_root(nullptr)
		{}

		bool Insert(const K& key, const V& value)
		{
			if (_root == nullptr)
			{
				_root = new Node(key, value);
				return true;
			}

			Node* parent = nullptr;
			Node* cur = _root;

			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			cur = new Node(key, value);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}

			return true;
		}

		Node* Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else
				{
					return cur;
				}
			}

			return nullptr;
		}

		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;

			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					// 找到，准备开始删除
					if (cur->_left == nullptr)
					{
						if (parent == nullptr)
						{
							_root = cur->_right;
						}
						else
						{
							if (parent->_left == cur)
								parent->_left = cur->_right;
							else
								parent->_right = cur->_right;
						}

						delete cur;
					}
					else if (cur->_right == nullptr)
					{
						if (parent == nullptr)
						{
							_root = cur->_left;
						}
						else
						{
							if (parent->_left == cur)
								parent->_left = cur->_left;
							else
								parent->_right = cur->_left;
						}

						delete cur;
					}
					else
					{
						Node* minParent = cur;
						Node* min = cur->_right;
						while (min->_left)
						{
							minParent = min;
							min = min->_left;
						}

						cur->_key = min->_key;
						cur->_value = min->_value;


						if (minParent->_left == min)
							minParent->_left = min->_right;
						else
							minParent->_right = min->_right;

						delete min;
					}

					return true;
				}
			}

			return false;
		}



		void InOrder()
		{
			_InOrder(_root);
			cout << endl;
		}

	private:
		void _InOrder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}

			_InOrder(root->_left);
			cout << root->_key << ":" << root->_value << endl;
			_InOrder(root->_right);
		}
	private:
		Node* _root;
	};
}

喜欢这篇文章的可以给个一键三连点赞👍关注💡收藏💖