数据结构中的排序算法--快速排序--C语言基础

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

快排的主流方法有三种

1.hoare版本

选最左边的数为参照对象key，指针left指向左边第一个数（下标为0），指针right指向右边第一个数（下标为n-1）,右边先走，遇到比key小的停下，再走左边，遇到比key大的停下，交换left与right所在位置，继续重复上述过程，直到left与right相遇，将key与相遇处交换。

选最右边的数为参照对象key，那么左边先走，遇大则停，右边再走，遇小则停，而这交换，循环此过程，直至二者相遇，交换key与相遇点。

上面是一趟排序，第一趟在key的左边都比key要小，key的右边都比key要大。那么继续将key的左边和右边分别看作新的无序序列进行排序，他们的范围则变成:[0,key-1],[key+1,N-1],找出新的key。直到left的下标大于或等于right的下标。

void Swap(int* px, int* py)
{
	int tmp = *px;
	*px = *py;
	*py = tmp;
}
//hoare版本
int Partion1(int* a, int left, int right)
{
	//三数取中--面对有序最坏情况，让中位数做key，变成最好情况
	int midi = GetMidIndex(a, left, right);
	Swap(&a[left], 

	//key在左边
	int keyi = left;
	while (left < right)
	{
		//右边先走，找小
		while (left < right&&a[right] >= a[keyi])
			--right;

		while (left < right && a[left] <= a[keyi])
			++left;
		Swap(&a[left], 
	}
	Swap(&a[left], 
	return left;
}
void QSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = Partion1(a, left, right);
	QSort(a, left, keyi - 1);
	QSort(a, keyi + 1, right);
}

 【总结】：

• 选最左边的值做key，右边先走-->左右相遇时比key小
• 选最右边的值做key，左边先走-->左右相遇时比key大

单趟排完，比key小的都放到了左边，比key大的都在右边，如果左子区间好的右子区间有序，整体就有序了。

发现每次排好的key值都在中间，假设每次选的key都是中位数

【最好】：高度的计算：每走一行走2^n，一共走要计算X个数，由等比数列和计算：2^n=X,n=logN(以2为底N的对数)

每次都要排N个数，所以时间复杂度O(N*logN)

【最坏】：有序数组从第一个数开始遍历，若按最左值为key值，从右面遍历，右面的值都比key要大，遍历了N趟，时间复杂度为O(N^2)

这是快排的一个缺陷，当排有序数组的时候，时间复杂度非常大。

所以为了解决这个问题，我们采取三数取中法，left，mid，right三个数里面取中间数作为key值

int GetMidIndex(int* a, int left, int right)
{
	//int mid = (left + right) / 2;
	int mid = left + ((right - left) >> 1);
	if (a[left] < a[mid])
	{
		if (a[right]<a[left])
		{
			return left;
		}
		else if (a[mid] < a[right])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
	else//a[left]>=a[mid]
	{
		if (a[right] > a[left])
		{
			return left;
		}
		else if (a[mid] > a[right])
		{
			return mid;
		}
		else
		{
			return right;
		}
	}
}

int Partion1(int* a, int left, int right)
{
	//三数取中--面对有序最坏情况，让中位数做key，变成最好情况
	int midi = GetMidIndex(a, left, right);
	Swap(&a[left], 
    
    //...
}

2.挖坑法

选取最左为key值，并将其变成坑位，left为最左值下标，right是最右值下标。左边为坑，从右开始走，右边找小，找到就放入左边的坑里，更新right的下标为坑。再走左边，左边找大，找到，放到右边的坑，更新找到的左值下标为坑，重复此过程，直到二者相遇，将key的值放入坑中，返回坑下标。

这样左边的值都比坑中key的值小，右边的值都比坑中key的值大。左边和右边的区域再重复上述过程。

//挖坑法
int Partion2(int* a, int left, int right)
{
	int mid = GetMidIndex(a, left, right);
	Swap(&a[mid], 

	int pivot = left;
	int keyi = left;
	//从右边开始，遇到小的放坑里，更新坑
	while (left < right)
	{
		while (left < right&&a[right] >= a[keyi])
		{
			right--;
		}
		a[pivot] = a[right];
		pivot = right;

		//走左边，遇到大的放坑里，更新坑
		while (left < right&&a[left] <= a[keyi])
		{
			left++;
		}
		a[pivot] = a[left];
		pivot = left;
	}
	//二者相遇跳出循环，key放坑
	a[pivot] = a[keyi];
	return pivot;
}
void QSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = Partion2(a, left, right);
	QSort(a, left, keyi - 1);
	QSort(a, keyi + 1, right);
}

3.前后指针版本

可以选取左边做key或右边做key

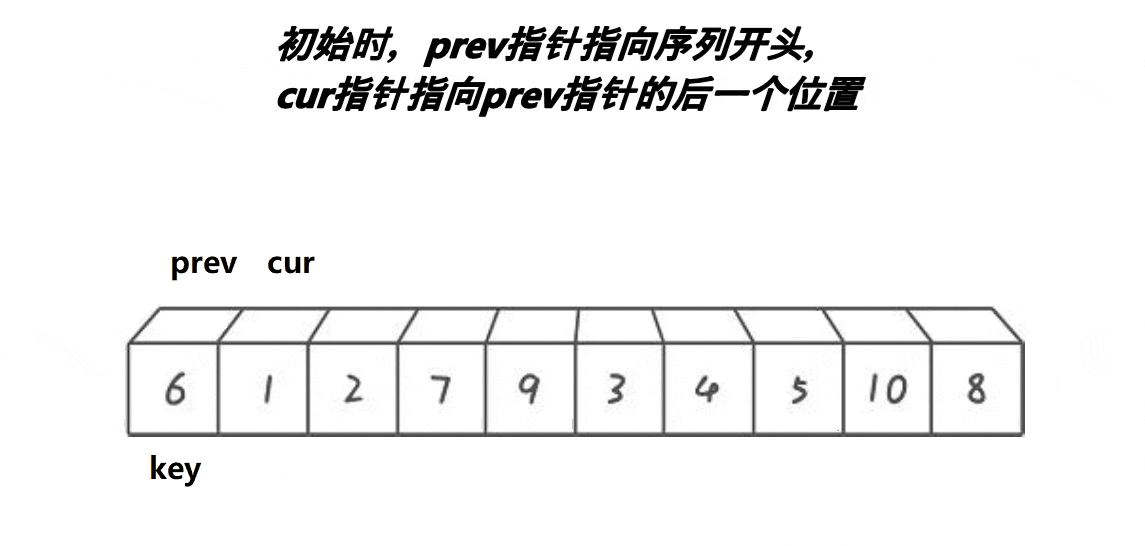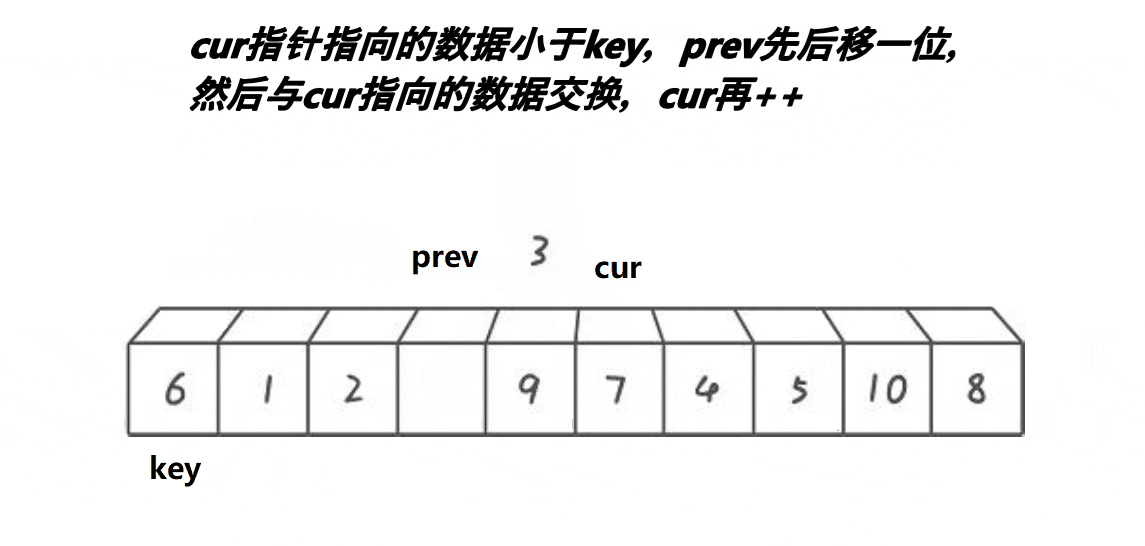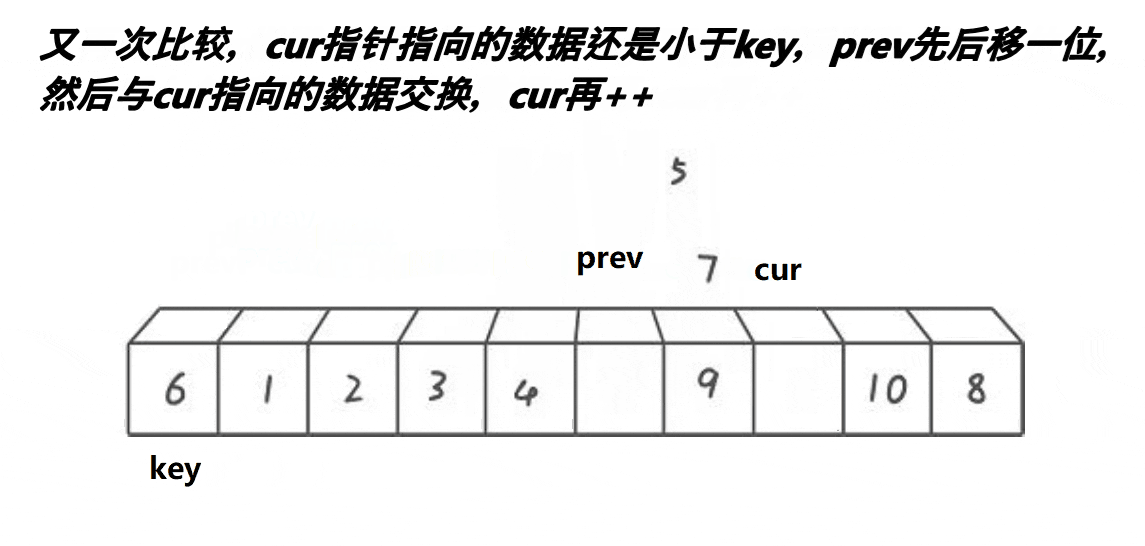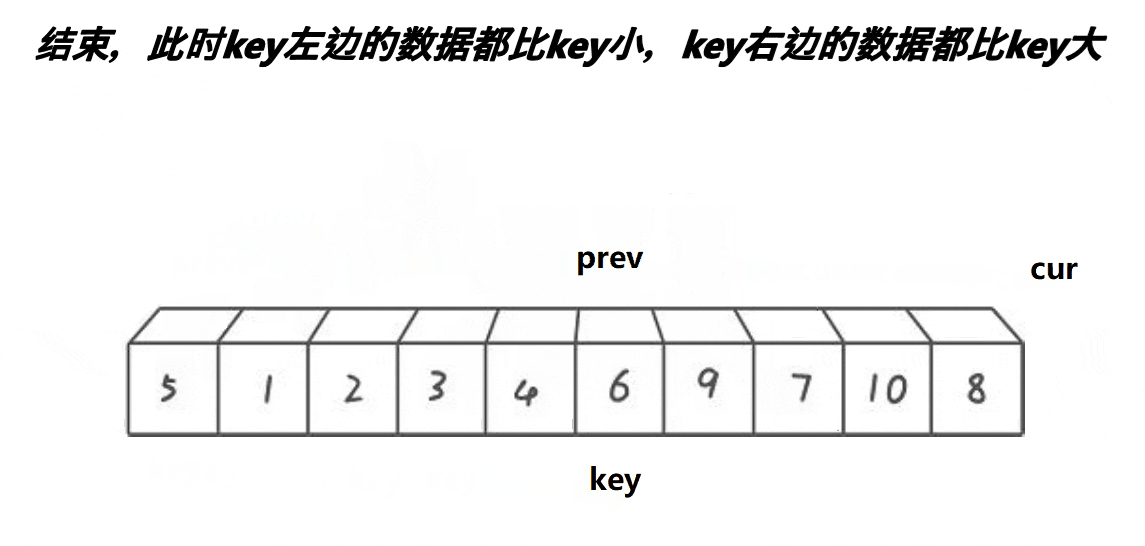
左边做key:这里使用两个指针prev和cur，当cur中的值比key小，那么cur和prev++交换，如果cur的值大于等于key，继续向下寻找。，直到cur遍历完整个数组。将key的值与prev交换。

右边做key:右边做key的时候，cur还是指向key的前一个，prev指向cur的后一个。和上面的过程一样，当cur大于等于key的值，向下寻找，找到比key小，prev++并与cur交换。但此时当cur遍历完整个数组，prev需要再++一下，再与key交换。

int Partion3(int* a, int left, int right)
{
	int keyi = left;
	int prev = left;
	int cur = left + 1;
	//当cur比key小，交换prev++和cur,找小
	while (cur <= right)
	{
		while (cur<=right && a[cur] >= a[keyi])
		{
			++cur;
		}
		if (cur > right)
			break;
		++prev;
		if (prev == cur)
		{
			cur++;
		}
		else
		{
			Swap(&a[prev], 
			++cur;
		}
	}
	Swap(&a[prev], 
	return prev;

	//int keyi = left;
	//int prev = left;
	//int cur = left + 1;
	//while (cur <= right)
	//{
	//	if (a[cur] < a[keyi] )//+prev != cur)
	//	{
	//		++prev;
	//		Swap(&a[cur], 
	//	}
	//	++cur;
	//}
	//Swap(&a[prev], 
	//return prev;
}
void QSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = Partion3(a, left, right);
	QSort(a, left, keyi - 1);
	QSort(a, keyi + 1, right);
}

4.非递归算法

【递归程序的缺陷】：

1.针对早期编译器，递归相比循环程序，性能差，因为对于递归调用，建立栈帧优化不大。现在编译器优化都很好，递归相比循环性能差不了多少

2.递归深度太深，会导致栈溢出，这也是为什么我们采用三数取中的方法。

非递归方法，运用到栈，因为要取到数组范围，将数组的第一个数和最后一个数依次放入栈中，因为栈的性质是先进后出，那么取到栈顶的数就是数组的最后一个数，将其删掉，再取便是数组第一个数，取到两个数就取到二者下标，对其进行排序，再将新的数组左右下标放入栈中，再次得到他的下标进行排序，直到左下标不小于右下标，循环停止。

相当于用到了中序遍历

//非递归
void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	StackInit(
	StackPush(
	StackPush(

	while (!StackEmpty(&st))
	{
		int end = StackTop(
		StackPop(

		int begin = StackTop(
		StackPop(

		int keyi = Partion3(a, begin, end);
		//[begin,keyi-1] keyi [keyi+1,end];
		if (begin < keyi - 1)
		{
			StackPush(
			StackPush(&st, keyi - 1);
		}
		if (keyi + 1 < end)
		{
			StackPush(&st, keyi + 1);
			StackPush(
		}
	}
    //malloc的空间需要释放一下
	StackDestroy(
}

栈的实现