最长公共子序列（动态规划）

一般使用动态规划的思路来解决该问题。因为涉及到子序列的问题，一般的话需要穷举出所有的可能结果。而动态规划的思路是穷举+去冗余，所以可以使用该思路解决。

动态规划考虑某一个解时，需要考虑之前所有的解。一般使用dp（动态规划数组）来保存所有出现的解。达到穷举后去冗余的效果。

1. 明确dp数组的含义

两个字符串的公共子串，那么二维数组dp结构：

2. 处理边缘值

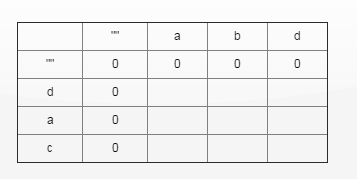
因为动态规划问题最终是要转换为公式计算，所以对于dp的边界要使用默认值处理。

3. 计算公式

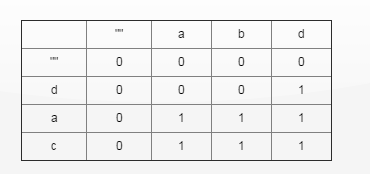
最终的数据填充：

设定两个字符串为S1和S2。

• 若S1i==S2j：那么最长公共子串为dp[i][j]=dp[i-1][j-1]+1;
• 若S1i!=S2j：那么为Max(dp[i-1][j],dp[i][j-1]);

为了解决边缘问题，dp[0][...]=0和dp[...][0]=0；

/** 
 * 给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列。 
 */  
public int longestCommonSubsequence(String text1, String text2) {  
    if (text1 == null || text2 == null || text1.length() == 0 || text2.length() == 0) {  
        return 0;  
    }  
    text1 = " " + text1;  
    text2 = " " + text2;  
    char[] s1 = text1.toCharArray();  
    char[] s2 = text2.toCharArray();  
    //创建dp数组  
    int[][] dp = new int[text1.length()][text2.length()];  
    //dp数组赋值。  
    for (int i = 0; i < text1.length(); i++) {  
        for (int j = 0; j < text2.length(); j++) {  
            //解决边缘值  
            if (i == 0 || j == 0) {  
                dp[i][j] = 0;  
                continue;  
            }  
            //获取到某位置的最大公共子序列长度  
            if (s1[i] == s2[j]) {  
                dp[i][j] = dp[i - 1][j - 1] + 1;  
            } else {  
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);  
            }  
        }  
    }  
    return dp[text1.length() - 1][text2.length() - 1];  
}