一、扩展:岭回归和Lasso
### --- 扩展:岭回归和Lasso
~~~ # 解决共线性的问题的方法主要有以下三种:
~~~ 其⼀是在建模之前对各特征进行相关性检验,若存在多重共线性,
~~~ 则可考虑进⼀步对数据集进行SVD分解或PCA主成分分析,
~~~ 在SVD或PCA执行的过程中会对数据集进行正交变换,
~~~ 最终所得数据集各列将不存在任何相关性。
~~~ 当然此举会对数据集的结构进行改变,且各列特征变得不可解释。~~~ 其⼆则是采用逐步回归的方法,以此选取对因变量解释力度最强的自变量,
~~~ 同时对于存在相关性的自变量加上⼀个惩罚因子,削弱其对因变量的解释力度,
~~~ 当然该方法不能完全避免多重共线性的存在,
~~~ 但能够绕过最小二乘法对共线性较为敏感的缺陷,构建线性回归模型。
~~~ 其三则是在原有的算法基础上进行修改,放弃对线性方程参数无偏估计的苛刻条件,
~~~ 使其能够容忍特征列存在多重共线性的情况,并且能够顺利建模,且尽可能的保证SSE取得最小值。
~~~ 通常来说,能够利用⼀个算法解决的问题尽量不用多个算的组合来解决,
~~~ 因此此处我们主要考虑后两个解决方案,其中逐步回归我们将放在线性回归的最后一部分进行讲解,
~~~ 而第三个解决方案,则是我们接下来需要详细讨论的岭回归算法和Lasso算法。二、岭回归
### --- 岭回归
~~~ # 基本原理
~~~ 岭回归算法实际上是针对线性回归算法局限性的⼀个改进类算法,
~~~ 优化目的是要解决系数矩阵XtX不可逆的问题,
~~~ 客观上同时也起到了克服数据集存在多重共线性的情况,
~~~ 而岭回归的做法也非常简单,就是在原方程系数计算公式中添加了⼀个扰动项入I,
~~~ 原先无法求广义逆的情况变成可以求出其广义逆,使得问题稳定并得以求解,
~~~ 其中 是自定义参数, 则是单位矩阵。
~~~ 岭回归在多元线性回归的损失函数上加上了正则项,
~~~ 表达为系数W的L2范式(即系数W的平方项)乘以正则化系数 。
~~~ 岭回归的损失函数的完整表达式写作: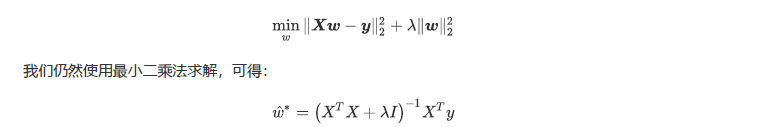
~~~ 此举看似简单,实则非常精妙,用⼀个满秩的对角矩阵和原系数矩阵计算进行相加,
~~~ 实际上起到了两个作用,其一是使得最终运算结果(XtX+入I)满秩,
~~~ 即降低了原数据集特征列的共线性影响,
~~~ 其二也相当于对所有的特征列的因变量解释程度进行了惩罚,且 越大惩罚作用越强。
~~~ 现在,只要(XtX+入I)存在逆矩阵,我们就可以求解出 。
~~~ 一个矩阵存在逆矩阵的充分必要条件是这个矩阵的行列式不为0。
~~~ 假设原本的特征矩阵中存在共线性,则我们的方阵XtX就会不满秩(存在全为零的行):


~~~ # 最后得到的这个行列式还是一个梯形行列式,然而它的已经不存在全0行或者全0列了,除非:
~~~ # 等于0
~~~ # 原本的矩阵XtX中存在对角线上元素为-入,其他元素都为0的行或者列
~~~ 否则矩阵XtX+入I永远都是满秩。在sklearn中, 的值我们可以自由控制,
~~~ 因此我们可以让它不为0,以避免第一种情况。
~~~ 而第二种情况,如果我们发现某个的取值下模型无法求解,
~~~ 那我们只需要换⼀个的取值就好了,也可以顺利避免。
~~~ 也就是说,矩阵的逆是永远存在的,有了这个保障,我们的W就可以写作: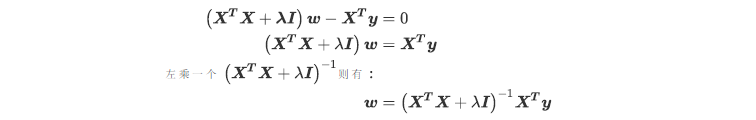
~~~ 如此,正则化系数就避免了”精确相关关系“带来的影响,
~~~ 至少最小二乘法在 存在的情况下是一定可以使用了。
~~~ 对于存在”高度相关关系“的矩阵,我们也可以通过调大 ,
~~~ 来让XtX+入I矩阵的行列式变大,从而让逆矩阵变小,以此控制参数向量W的偏移。
~~~ 当入越大,模型越不容易受到共线性的影响。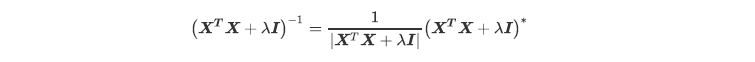
~~~ 如此,多重共线性就被控制住了:最小二乘法⼀定有解,并且这个解可以通过 来进行调节,
~~~ 以确保不会偏离太多。
~~~ 当然了, 挤占了W中由原始的特征矩阵贡献的空间,
~~~ 因此 如果太大,也会导致W的估计出现较大的偏移,无法正确拟合数据的真实面貌。
~~~ 我们在使用中,需要找出 让模型效果变好的最佳取值。### --- Python实践
~~~ 接下来,尝试在Python中手动编写岭回归函数,
~~~ 当然在借助矩阵运算的情况下岭回归函数的编写也不会太复杂,
~~~ 这里唯⼀需要注意的是对于单位矩阵的⽣成,
~~~ 需要借助Numpy中的eye函数,该函数需要输入对角矩阵规模参数。
~~~ 虽说是生成单位矩阵,但实际上返回的仍然是array对象,若要真正意义上执行矩阵运算,
~~~ 则还需要进行矩阵转化,接下来编写岭回归函数,此处默认设置岭回归系数为0.2,
~~~ 当该系数不为0的时候不会存在不可逆的情况,因此可免去 if 语句判别是否满秩的设置。def ridgeRegres(dataSet,lam=0.2):
xMat = np.mat(dataSet.iloc[:,:-1].values)
yMat = np.mat(dataSet.iloc[:,-1].values).T
xTx = xMat.T * xMat
denom = xTx + np.eye(xMat.shape[1])*lam
ws = denom.I * (xMat.T * yMat)
return ws~~~ 然后读取 abalone 数据集进行岭回归建模,该数据集源于UCI,
~~~ 记录了鲍⻥的生物属性,目标字段是鲍⻥的年龄:
aba = pd.read_csv('abalone.csv',header=None)
aba.head()~~~ 其中⼀列为标签列,同时,由于数据集第⼀列是分类变量,且没有用于承载截距系数的列。
~~~ 为了简化教学流程,此处直接将第⼀列的值全部修改为1,然后在进行建模:
aba.iloc[:,0]=1
aba.head()~~~ 接着带入模型进行计算并返回各列系数:
rws = ridgeRegres(aba)
rws
~~~ 由于数据集本身性质满足最小二乘法求解条件,因此可对比最小⼆乘法求解结果:
standRegres(aba)~~~ 能够发现由于惩罚因子存在,最终输出结果存在细微差别。同时我们可比较二者模型的评价指标:
rSquare(aba,ridgeRegres)
rSquare(aba,standRegres)~~~ 这里由于数据集本身性质原因,岭回归和线性回归返回结果并没有太大区别。
~~~ 接下来,调用scikit-learn中岭回归算法验证手动建模有效性。
from sklearn.linear_model import Ridge
ridge = Ridge(alpha = 0.2)
ridge.fit(aba.iloc[:,:-1],aba.iloc[:,-1])~~~ 查看模型相关参数:
ridge.coef_ #查看系数
ridge.intercept_ # 查看截距~~~ 对比手动建模结果,能够看出结果基本保持⼀致。
~~~ 接着我们使用交叉验证来选择最佳的正则化系数。
~~~ 在scikit-learn中,我们有带交叉验证的岭回归可以使用,我们来看⼀看:
class sklearn.linear_model.RidgeCV (alphas=(0.1, 1.0, 10.0), fifit_intercept=True,
normalize=False,scoring=None, cv=None, gcv_mode=None, store_cv_values=False)
~~~ 可以看到,这个类与普通的岭回归类Ridge非常相似,
~~~ 不过在输入正则化系数 的时候我们可以传入元组作为正则化系数的备选,
~~~ 非常类似于我们在画学习曲线前设定的for i in 的列表对象。来看RidgeCV的重要参数,属性和接口:重要参数 | 含义 |
alphas | 需要测试的正则化参数的取值的元组 |
scoring | 用来进行交叉验证的模型评估指标,默认是R2,可自行调整 |
store_cv_values | 是否保存每次交叉验证的结果,默认False |
cv | 交叉验证的模式,默认是None,表示默认进行留⼀交叉验证可以输⼊fold对象和StratififiedKFold对象来进行交叉验证注意,仅仅当为None时, 每次交叉验证的结果才可以被保存下来当cv有值存在(不是None)时, store_cv_values⽆法被设定为True |
重要属性 | 含义 |
alpha_ | 查看交叉验证选中的alpha |
cv_values_ | 调用所有交叉验证的结果, 只有当store_cv_values=True的时候才能够调用, 因此返回的结构是(n_samples, n_alphas) |
重要接口 | 含义 |
score | 调用Ridge类不进行交叉验证的情况下返回的平方 |
### --- 这个类的使也用非常容易,依然使用我们之前建立的鲍鱼年龄数据集:
from sklearn.linear_model import RidgeCV
Ridge_ = RidgeCV(alphas=np.arange(1,1001,100)
,scoring="r2"
,store_cv_values=True
#,cv=5
).fit(aba.iloc[:,:-1],aba.iloc[:,-1])
#⽆关交叉验证的岭回归结果
Ridge_.score(aba.iloc[:,:-1],aba.iloc[:,-1])
#调⽤所有交叉验证的结果
Ridge_.cv_values_.shape
#进⾏平均后可以查看每个正则化系数取值下的交叉验证结果
Ridge_.cv_values_.mean(axis=0)
#查看被选择出来的最佳正则化系数
Ridge_.alpha_三、Lasso
### --- Lasso
~~~ # 基本原理
~~~ 在岭回归中,对自变量系数进行平方和处理也被称作L2正则化,
~~~ 由于此原因,领回归中自变量系数虽然会很快衰减,但很难归为零,
~~~ 且存在共线性的时候衰减过程也并非严格递减,这就是为何岭回归能够建模、判断共线性,
~~~ 但很难进行变量筛选的原因。
~~~ 为了弥补岭回归在这方面的不足,Tibshirani(1996)提出了Lasso (The Least Absolute Shrinkage and Selectionatoroperator)算法,
~~~ 将岭回归的损失函数中的自变量系数L2正则化修改为L1正则化,即Lasso回归损失函数为∶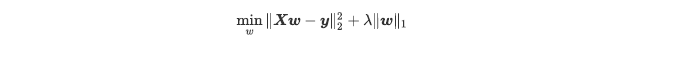
~~~ 我们来看看Lasso的计算过程。当我们使用最小二乘法来求解Lasso中的参数 ,
~~~ 我们依然对损失函数进行求导:
~~~ 现在问题又回到了要求XtX的逆必须存在。
~~~ 在岭回归中,我们通过正则化系数 能够向方阵XtX加上⼀个单位矩阵,
~~~ 以此来防止方阵XtX的行列式为0,而现在L1范式所带的正则项 在求导之后并不带有W这个项,
~~~ 因此它无法对XtX造成任何影响。也就是说,Lasso无法解决特征之间”精确相关“的问题。
~~~ 当我们使用最小二乘法求解线性回归时,
~~~ 如果线性回归无解或者报除零错误,换Lasso不能解决任何问题。岭回归 vs Lasso |
岭回归可以解决特征间的精确相关关系导致的最小二乘法无法使用的问题,而Lasso不⾏。 |
~~~ 不过,在现实中我们其实会比较少遇到“精确相关”的多重共线性问题,
~~~ 大部分多重共线性问题应该是“高度相关“,
~~~ 而如果我们假设方阵XtX的逆是⼀定存在的,那我们可以有: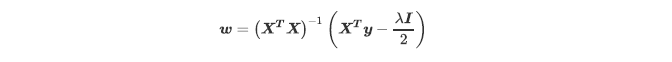
~~~ 通过增大 ,我们可以为W的计算增加⼀个负项,从而限制参数估计中W的大小,
~~~ 而防止多重共线性引起的参数W被估计过⼤导致模型失准的问题。
~~~ Lasso不是从根本上解决多重共线性问题,是限制多重共线性带来的影响。### --- Python实现
~~~ 接下来,尝试在scikit-learn中执行Lasso算法,仍然是采用abalone数据集,
~~~ Lasso算法模型也同样是保存在linear_model模块中。
from sklearn.linear_model import Lasso
las = Lasso(alpha=0.01)
las.fit(aba.iloc[:,:-1],aba.iloc[:,-1])~~~ # 查看执行结果
~~~ 不同于岭回归,Lasso算法的处理结果中自变量系数会更加倾向于迅速递减为0,
~~~ 因此Lasso算法在自变量选择方面要优于岭回归。
~~~ 能够看出Lasso回归自变量衰减速度非常快,
~~~ 当入取0.01的时候就已经出现部分自变量系数为0的情况,从中也能看出自变量的相对重要性。
las.coef_
las.intercept_四、总结
### --- 总结
~~~ 多元线性回归,岭回归,Lasso三个算法,它们都是围绕着原始的线性回归进行的拓展和改进。
~~~ 其中岭回归和Lasso是为了解决多元线性回归中使用最小二乘法的各种限制,
~~~ 主要用途是消除多重共线性带来的影响并且做特征选择。
~~~ 除此之外,本章还定义了多重共线性和各种线性相关的概念,并为大家补充了一些线性代数知识。
~~~ 回归算法属于原理简单,但操作困难的机器学习算法,在实践和理论上都还有很长的路可以走。Walter Savage Landor:strove with none,for none was worth my strife.Nature I loved and, next to Nature, Art:I warm'd both hands before the fire of life.It sinks, and I am ready to depart
——W.S.Landor










